Hostname: page-component-599cfd5f84-v8j7l Total loading time: 0 Render date: 2025-01-07T07:23:41.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of limit cycles for a class of autonomous systems

Published online by Cambridge University Press:  17 April 2009

Anthony Sofo
Anthony Sofo
Affiliation:
Department of Applied Mathematics, La Trobe University, Bundoora, Victoria 3083, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A proof is given for the existence of at least one stable periodic limit cycle solution for the polynomial non-linear differential equation of the form

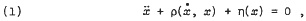
in some cases where the Levinson-Smith criteria are not directly applicable.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 28 , Issue 3 , December 1983 , pp. 331 - 337
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Andronov, A.A., Leontovich, E.A., Gordon, I.I. and Maier, A.G., Qualitative theory of second-order dynamic systems (John Wiley & Sons, New York, London, 1973).Google Scholar
[2]Dragilev, A.D., “Periodic solutions of the differential equation of non-linear oscillations”, Prikl. Mat. Meh. 12 (1952), 85–88.Google Scholar
[3]Levinson, N. and Smith, O.K., “A general equation for relaxation oscillations”, Duke Math. J. 9 (1942), 382–403.Google Scholar
[4]Minorsky, N., Nonlinear oscillations (Van Nostrand, Princeton, 1962).Google Scholar
[5]Zandt, J. Parker Van, “Oscillating systems by resistance proportional to the square of the velocity”, Phys. Rev. 15 (1919), 415–443.Google Scholar
[6]Poincaré, H., Oeuvres (Gauthier-Villars, Paris, 1928).Google Scholar
[7]Reissig, R., “Selbsterregung eines einfachen Schwingers”, Math. Nachr. 15 (1956), 191–196.Google Scholar
[8]Sansoni, G. and Conti, R., Non-linear differential equations (Macmillan, New York, 1964).Google Scholar
[9]Villari, G., “On the existence of periodic solutions for Lienard's equation”, Nonlin. Anal. 7 (1983), 71–78.CrossRefGoogle Scholar
[10]Zhifen, Z., “Theorem of existence of exact n limit cycles in |x| ≤ (n+1) for the differential equation x + sin x + x = 0” Sci. Sinica 23 (1980), 1502–1510.Google Scholar