Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Figueiredo, D. G.
and
Ding, Y. H.
2002.
Djairo G. de Figueiredo - Selected Papers.
p.
517.
Li, Gongbao
and
Yang, Jianfu
2004.
Asymptotically Linear Elliptic Systems.
Communications in Partial Differential Equations,
Vol. 29,
Issue. 5-6,
p.
925.
Peng, Chaoquan
2011.
Asymptotically linear elliptic systems inRN.
Journal of Mathematical Analysis and Applications,
Vol. 380,
Issue. 2,
p.
540.
Zhang, Qingye
and
Wang, Qi
2012.
Multiple solutions for a class of sublinear Schrödinger equations.
Journal of Mathematical Analysis and Applications,
Vol. 389,
Issue. 1,
p.
511.
Souza, Manassés de
2012.
On a singular Hamiltonian elliptic systems involving critical growth in dimension two.
Communications on Pure and Applied Analysis,
Vol. 11,
Issue. 5,
p.
1859.
Li, Gongbao
and
Wang, Chunhua
2013.
Multiple solutions for a semilinear elliptic system in .
Mathematical Methods in the Applied Sciences,
Vol. 36,
Issue. 18,
p.
2456.
Tang, X.H.
2013.
Infinitely many solutions for semilinear Schrödinger equations with sign-changing potential and nonlinearity.
Journal of Mathematical Analysis and Applications,
Vol. 401,
Issue. 1,
p.
407.
Qin, Dongdong
and
Tang, Xianhua
2016.
Solutions on Asymptotically Periodic Elliptic System with New Conditions.
Results in Mathematics,
Vol. 70,
Issue. 3-4,
p.
539.
Albuquerque, Francisco S. B.
do Ó, João Marcos
and
Medeiros, Everaldo S.
2016.
On a class of Hamiltonian elliptic systems involving unbounded or decaying potentials in dimension two.
Mathematische Nachrichten,
Vol. 289,
Issue. 13,
p.
1568.
Tang, Xianhua
and
Zhang, Jian
2017.
Ground state solutions of Nehari‐Pankov type for a superlinear elliptic system on .
Mathematical Methods in the Applied Sciences,
Vol. 40,
Issue. 3,
p.
729.
Qin, Dongdong
Chen, Jing
and
Tang, XianHua
2017.
Existence and non-existence of nontrivial solutions for Schrödinger systems via Nehari–Pohozaev manifold.
Computers & Mathematics with Applications,
Vol. 74,
Issue. 12,
p.
3141.
Cheng, Rong
and
Wu, Yijia
2020.
Remarks on infinitely many solutions for a class of Schrödinger equations with sublinear nonlinearity.
Mathematical Methods in the Applied Sciences,
Vol. 43,
Issue. 15,
p.
8527.
My, Bui Kim
2022.
Results on the Existence and Multiplicity of Solutions for a Class of Sublinear Degenerate Schrödinger Equations in $$\mathbb{R}^N$$.
Mathematical Notes,
Vol. 112,
Issue. 5-6,
p.
845.


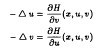
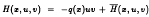 with
with 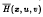 (
(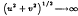 .
.