Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T05:59:51.806Z Has data issue: false hasContentIssue false
  • English
  • Français

EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA

Part of: Modules, bimodules and ideals Rings and algebras with additional structure

Published online by Cambridge University Press:  23 August 2021

LIA VAŠ Open the ORCID record for LIA VAŠ [Opens in a new window]
LIA VAŠ*
Affiliation:
Department of Mathematics, Physics and Statistics, University of the Sciences, Philadelphia, PA19104, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that every graded ideal of a Leavitt path algebra is graded isomorphic to a Leavitt path algebra. It is known that a graded ideal I of a Leavitt path algebra is isomorphic to the Leavitt path algebra of a graph, known as the generalised hedgehog graph, which is defined based on certain sets of vertices uniquely determined by I. However, this isomorphism may not be graded. We show that replacing the short ‘spines’ of the generalised hedgehog graph with possibly fewer, but then necessarily longer spines, we obtain a graph (which we call the porcupine graph) whose Leavitt path algebra is graded isomorphic to I. Our proof can be adapted to show that, for every closed gauge-invariant ideal J of a graph 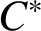$C^*$ -algebra, there is a gauge-invariant $*$ -isomorphism mapping the graph 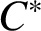$C^*$ -algebra of the porcupine graph of J onto 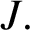$J.$

Keywords

Leavitt path algebragraded ringgraded ideal

MSC classification

Secondary: 16D25: Ideals 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation 16W50: Graded rings and modules
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 2 , April 2022 , pp. 248 - 256
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrams, G., Ara, P. and Siles Molina, M., Leavitt Path Algebras, Lecture Notes in Mathematics, 2191 (Springer, London, 2017).CrossRefGoogle Scholar
Aranda Pino, G., Rangaswamy, K. M. and Siles Molina, M., ‘Weakly regular and self-injective Leavitt path algebras over arbitrary graphs’, Algebr. Represent. Theory 14 (2011), 751–777.CrossRefGoogle Scholar
Bates, T., Hong, J. H., Raeburn, I. and Szymański, W., ‘The ideal structure of the ${C}^{\ast }$ -algebras of infinite graphs’, Illinois J. Math. 46(4) (2002), 1159–1176.CrossRefGoogle Scholar
Hazrat, R., Graded Rings and Graded Grothendieck Groups, London Mathematical Society Lecture Note Series, 435 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Ruiz, E. and Tomforde, M., ‘Ideals in graph algebras’, Algebr. Represent. Theory 17(3) (2014), 849–861.10.1007/s10468-013-9421-3CrossRefGoogle Scholar
Tomforde, M., ‘Uniqueness theorems and ideal structure for Leavitt path algebras’, J. Algebra 318(1) (2007), 270–299.10.1016/j.jalgebra.2007.01.031CrossRefGoogle Scholar
Vaš, L., ‘Canonical traces and directly finite Leavitt path algebras’, Algebr. Represent. Theory 18 (2015), 711–738.CrossRefGoogle Scholar