No CrossRef data available.
Published online by Cambridge University Press: 31 July 2023
For an integer 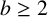 $b\geq 2$, a positive integer is called a b-Niven number if it is a multiple of the sum of the digits in its base-b representation. In this article, we show that every arithmetic progression contains infinitely many b-Niven numbers.
$b\geq 2$, a positive integer is called a b-Niven number if it is a multiple of the sum of the digits in its base-b representation. In this article, we show that every arithmetic progression contains infinitely many b-Niven numbers.