Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-22T05:58:41.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimation of the integral of a stochastic process

Published online by Cambridge University Press:  17 April 2009

Noel Cressie
Noel Cressie
Affiliation:
School of Mathematical Sciences, Flinders University, Bedford Park, South Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the class of stochastic processes with stationary independent increments and finite variances; notable members are brownian motion, and the Poisson process. Now for Xt any member of this class of processes, we wish to find the optimum sampling points of Xt, for predicting 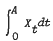. This design question is shown to be directly related to finding sampling points of Yt for estimating β in the regression equation, Yt = β + Xt. Since processes with stationary independent increments have linear drift, the regression equation for Yt is the first type of departure we might look for; namely quadratic drift, and unchanged covariance structure.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 18 , Issue 1 , February 1978 , pp. 83 - 93
Copyright
Copyright © Australian Mathematical Society 1978

References

[1]Sacks, Jerome and Ylvisaker, Donald, “Statistical designs and integral approximation”, Time series and stochastic processes; convexity and combinatorics, 115–136 (Proc. Twelfth Biennial Seminar, Canadian Mathematical Congress, University of British Columbia, 1969. Canadian Mathematical Congress, Société Mathématique du Canada, Montreal, Canada, 1970).Google Scholar