No CrossRef data available.
Article contents
Erratum: Two hyperbolic Shwarz lemmas
Published online by Cambridge University Press: 17 April 2009
Extract
In [1] there is an error, as pointed out to us by J.M. Isidro. In that paper we consider the set Rm of all m-rotations, that is, Rm = {czm: |c| = 1}; the set Aut() of the automorphisms of the unit disc and the set of the m-automorphisms of , Autm () = {ψ ∘ R ∘ ϕ : ψ, ϕ ∈ Aut(), R ∈ Rm}. We asserted that
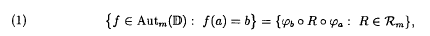
where ϕa(Z) = (a − z)/(1 − āz). Equality (1) is not true. For instance, it suffices to consider f (z) = ϕ¼ ∘ ∘ z2 ∘ ϕ½. We have that f ∈ Aut2 (), f (0) = (0) and, after calculations, f (z) = (7z2 − 6z)/(6z − 7). Then it is evident that will never hold f (z) = ϕ0 ∘ R ∘ ϕ0 with R ∈ R2, because ϕ0 is equal to identity.
- Type
- Correction
- Information
- Copyright
- Copyright © Australian Mathematical Society 2003


