Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T15:30:22.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding group amalgams

Published online by Cambridge University Press:  17 April 2009

Patrick Fitzpatrick  and
James Wiegold
Patrick Fitzpatrick
Affiliation:
Department of Mathematics, University College, Cork, Ireland;
James Wiegold
Affiliation:
Department of Pure Mathematics, University College, PO Box 78, Cardiff CFI IXL, Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A class 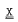of groups is said to have the small embedding property if every amalgam of two groups from 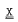amalgamating a normal subgroup embeds into a group not generating the variety 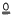of all groups. Very few large classes have the small embedding property. For example, the minimal non-abelian varieties containing non-abelian finite groups do not; neither does any class of groups containing 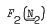; but the set of finitely generated groups in a nilpotent variety not containing 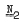does have the small embedding property.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 24 , Issue 3 , December 1981 , pp. 373 - 379
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Jones, Gareth A., “Varieties and simple groups”, J. Austral. Math. Soc. 17 (1974), 163–173.CrossRefGoogle Scholar
[2]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 37. Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[3]Wiegold, James, “Soluble embeddings of group amalgams”, Publ. Math. Debrecen 12 (1965), 227–230.CrossRefGoogle Scholar