Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T11:24:15.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic integrals and limit cycles

Published online by Cambridge University Press:  17 April 2009

A.M. Urbina ,
M. León De La Barra ,
G. León De La Barra  and
M. Cañas
A.M. Urbina
Affiliation:
Universidad Técnica, Federico Santa María Departamento de Matemática Casilla 110 – V Valparaíso, Chile
M. León De La Barra
Affiliation:
Universidad Técnica, Federico Santa María Departamento de Matemática Casilla 110 – V Valparaíso, Chile
G. León De La Barra
Affiliation:
Universidad Técnica, Federico Santa María Departamento de Matemática Casilla 110 – V Valparaíso, Chile
M. Cañas
Affiliation:
Universidad Técnica, Federico Santa María Departamento de Matemática Casilla 110 – V Valparaíso, Chile
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By using zeros of elliptic integrals we establish an upper bound for the number of limit cycles that emerge from the period annulus of the Hamiltonian XH in the system Xε = XH + ε(P, Q), where H = y2 + x4 and P, Q are polynomials in x, y, as a function of the degrees of P and Q. In particular, if (P, Q) = 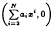, with N = 2k + 1 or 2k + 2, this upper bound is k − 1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 48 , Issue 2 , October 1993 , pp. 195 - 200
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Chicone, C. and Jacobs, M., ‘Bifurcation of limit cycles from quadratic isochrones’, J. Differential Equations 91 (1991), 268–326.CrossRefGoogle Scholar
[2]Poincaré, H., ‘Sur les courbes définies par une equation differéntielle’, J. Mathematique 7 (1881), 375–422.Google Scholar
[3]Petrov, G.S., ‘Number of zeros of complete elliptic integrals’, Functional Anal. Appl. 18 (1984), 148–150.CrossRefGoogle Scholar
[4]Petrov, G.S., ‘Elliptic integrals and their monoscillation’, Functional Anal. Appl. 20 (1986), 37–40.Google Scholar
[5]Petrov, G.S., ‘Complex zeros of an elliptic integral’, Functional Anal. Appl. 21 (1987), 247–248.CrossRefGoogle Scholar
[6]Rosseau, C. and Zoladek, H., ‘Zeros of Complete Elliptic Integrals for 1:2 Resonance’, J. Differential Equations 94 (1991), 41–54.CrossRefGoogle Scholar
[7]Urbina, A., León de la Barra, G., León de la Barra, M. and Cañas, M., ‘Limit cycles of Liénard equations with not linear damping’, Canad. Math. Bull, (to appear)Google Scholar
[8]Varchenko, A.N., ‘Estimate of the number of zeros of abelian integrals depending on parameters and limit cycles’, Functional Anal. Appl. 18 (1984), 98–108.CrossRefGoogle Scholar