No CrossRef data available.
Published online by Cambridge University Press: 20 August 2012
Let 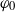 $\varphi _0$ and
$\varphi _0$ and 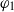 $\varphi _1$ be regular functions on the boundary
$\varphi _1$ be regular functions on the boundary 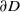 $\partial D$ of the unit disk
$\partial D$ of the unit disk 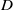 $D$ in
$D$ in 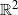 $\mathbb {R}^2$, such that
$\mathbb {R}^2$, such that 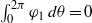 $\int _{0}^{2\pi }\varphi _1\,d\theta =0$ and
$\int _{0}^{2\pi }\varphi _1\,d\theta =0$ and 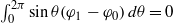 $\int _{0}^{2\pi }\sin \theta (\varphi _1-\varphi _0)\,d\theta =0$. It is proved that there exist a linear second-order uniformly elliptic operator
$\int _{0}^{2\pi }\sin \theta (\varphi _1-\varphi _0)\,d\theta =0$. It is proved that there exist a linear second-order uniformly elliptic operator 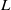 $L$ in divergence form with bounded measurable coefficients and a function
$L$ in divergence form with bounded measurable coefficients and a function  $u$ in
$u$ in 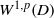 $W^{1,p}(D)$,
$W^{1,p}(D)$, 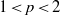 $1 \lt p \lt 2$, such that
$1 \lt p \lt 2$, such that 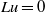 $Lu=0$ in
$Lu=0$ in 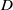 $D$ and with
$D$ and with 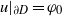 $u|_{\partial D}= \varphi _0$ and the conormal derivative
$u|_{\partial D}= \varphi _0$ and the conormal derivative 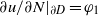 $\partial u/\partial N|_{\partial D}=\varphi _1$.
$\partial u/\partial N|_{\partial D}=\varphi _1$.