Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T13:33:54.006Z Has data issue: false hasContentIssue false
  • English
  • Français

DUAL DIFFERENTIATION SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  28 March 2019

WARREN B. MOORS  and
NEŞET ÖZKAN TAN
WARREN B. MOORS*
Affiliation:
Department of Mathematics, The University of Auckland, Auckland 1142, New Zealand email [email protected]
NEŞET ÖZKAN TAN
Affiliation:
Department of Mathematics, The University of Auckland, Auckland 1142, New Zealand email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 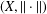$(X,\Vert \cdot \Vert )$ is a Banach space that admits an equivalent locally uniformly rotund norm and the set of all norm-attaining functionals is residual then the dual norm 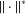$\Vert \cdot \Vert ^{\ast }$ on 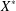$X^{\ast }$ is Fréchet at the points of a dense subset of $X^{\ast }$. This answers the main open problem in a paper by Guirao, Montesinos and Zizler [‘Remarks on the set of norm-attaining functionals and differentiability’, Studia Math.241 (2018), 71–86].

Keywords

norm-attaining functionalslocally uniformly rotund normdual differentiation space

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B26: Nonseparable Banach spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 467 - 472
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Bishop, E. and Phelps, R. R., ‘A proof that every Banach space is subreflexive’, Bull. Amer. Math. Soc. (N.S.) 67 (1961), 97–98.Google Scholar
Giles, J. R. and Kenderov, P. S., ‘On the structure of Banach spaces with Mazur’s intersection property’, Math. Ann. 291 (1991), 463–471.Google Scholar
Giles, J. R., Kenderov, P. S., Moors, W. B. and Sciffer, S. D., ‘Generic differentiability of convex functions on the dual of a Banach space’, Pacific J. Math. 172(2) (1996), 413–431.Google Scholar
Giles, J. R. and Moors, W. B., ‘Differentiability properties of Banach spaces where the boundary of the closed unit ball has denting point properties’, in: Miniconference on Probability and Analysis (Sydney, 1991), Proceedings of the Centre for Mathematics and its Applications, 29 (Australian National University, Canberra, 1992), 107–115.Google Scholar
Giles, J. R. and Moors, W. B., ‘The implications for differentiability theory of a weak index of non-compactness’, Bull. Aust. Math. Soc. 48 (1993), 85–101.Google Scholar
Giles, J. R. and Moors, W. B., ‘A continuity property related to Kuratowski’s index of non-compactness, its relevance to the drop property and its implications for differentiability theory’, J. Math. Anal. Appl. 178 (1993), 247–268.Google Scholar
Guirao, A. J., Montesinos, V. and Zizler, V., ‘Remarks on the set of norm-attaining functionals and differentiability’, Studia Math. 241 (2018), 71–86.Google Scholar
Kenderov, P. S., Kortezov, I. and Moors, W. B., ‘Norm continuity of weakly continuous mappings into Banach spaces’, Topology Appl. 153 (2006), 2745–2759.Google Scholar
Kenderov, P. S. and Moors, W. B., ‘A dual differentiation space without an equivalent locally uniformly rotund norm’, J. Aust. Math. Soc. A 77 (2004), 357–364.Google Scholar
Kenderov, P. S. and Moors, W. B., ‘Separate continuity, joint continuity and the Lindelöf property’, Proc. Amer. Math. Soc. 134 (2006), 1503–1512.Google Scholar
Molto, A., Orihuela, J., Troyanski, S. and Valdivia, M., ‘On weakly locally uniformly rotund Banach spaces’, J. Funct. Anal. 163 (1999), 252–271.Google Scholar
Moors, W. B., ‘A continuity property related to an index of non-separability and its applications’, Bull. Aust. Math. Soc. 46 (1992), 67–79.Google Scholar
Moors, W. B., ‘The relationship between Goldstine’s theorem and the convex point of continuity property’, J. Math. Anal. Appl. 188 (1994), 819–832.Google Scholar
Moors, W. B., ‘A gentle introduction to James’ weak compactness theorem and beyond’, Methods Funct. Anal. Topology 25(1) (2019), to appear.Google Scholar
Moors, W. B. and Giles, J. R., ‘Generic continuity of minimal set-valued mappings’, J. Aust. Math. Soc. A 63 (1997), 238–262.Google Scholar
Phelps, R. R., Convex Functions, Monotone Operators and Differentiability, 2nd edn, Lecture Notes in Mathematics, 1364 (Springer, Berlin, 1993).Google Scholar