Published online by Cambridge University Press: 17 April 2009
Let G be a doubly transitive permutation group on a finite set Ω, and for α in Ω suppose that Gα has a set Σ of non-trivial blocks of imprimitivity in Ω - {α}. If Gα is 2-transitive but not faithful on Σ, when is it true that the stabiliser in Gα of a block of Σ does not act faithfully on that block (that is, there is a nontrivial element in Gα which fixes every point of the block)? In a previous paper this question was answered when 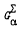 is the alternating or symmetric group, or a Mathieu group in its usual representation. In this paper we answer the question when
is the alternating or symmetric group, or a Mathieu group in its usual representation. In this paper we answer the question when 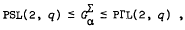 , permuting the q + 1 points of the projective line, for some prime power q. We show that the only groups which arise satisfy either
, permuting the q + 1 points of the projective line, for some prime power q. We show that the only groups which arise satisfy either
(i) PSL(3, q) ≤ G ≤ PΓL(3, q) in its natural representation, or
(ii) G is a group of collineations of an affine translation plane of order q, and contains the translation group.