No CrossRef data available.
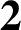 $\textbf{2}$ AND
$\textbf{2}$ AND 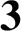 $\textbf{3}$
$\textbf{3}$Published online by Cambridge University Press: 14 January 2021
Andrews introduced the partition function
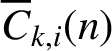 $\overline {C}_{k, i}(n)$
, called the singular overpartition function, which counts the number of overpartitions of n in which no part is divisible by k and only parts
$\overline {C}_{k, i}(n)$
, called the singular overpartition function, which counts the number of overpartitions of n in which no part is divisible by k and only parts
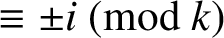 $\equiv \pm i\pmod {k}$
may be overlined. We prove that
$\equiv \pm i\pmod {k}$
may be overlined. We prove that
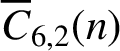 $\overline {C}_{6, 2}(n)$
is almost always divisible by
$\overline {C}_{6, 2}(n)$
is almost always divisible by
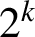 $2^k$
for any positive integer k. We also prove that
$2^k$
for any positive integer k. We also prove that
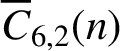 $\overline {C}_{6, 2}(n)$
and
$\overline {C}_{6, 2}(n)$
and
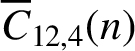 $\overline {C}_{12, 4}(n)$
are almost always divisible by
$\overline {C}_{12, 4}(n)$
are almost always divisible by
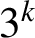 $3^k$
. Using a result of Ono and Taguchi on nilpotency of Hecke operators, we find infinite families of congruences modulo arbitrary powers of
$3^k$
. Using a result of Ono and Taguchi on nilpotency of Hecke operators, we find infinite families of congruences modulo arbitrary powers of
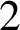 $2$
satisfied by
$2$
satisfied by
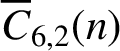 $\overline {C}_{6, 2}(n)$
.
$\overline {C}_{6, 2}(n)$
.