Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T10:32:08.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisibility of binary relations

Published online by Cambridge University Press:  17 April 2009

D.G. Fitz-Gerald  and
G.B. Preston
D.G. Fitz-Gerald
Affiliation:
Monash University, Clayton, Victoria.
G.B. Preston
Affiliation:
Monash University, Clayton, Victoria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

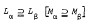In his paper in Mat. Sb. (N.S.) 61 (103) (1963), Zareckiĭ associated with any binary relation α an ordered pair, (Lα Mα), say, of lattices and showed that α is a left [right] divisor of β if and only if We provide an alternative proof of this result by embedding the category of relations in the category of sets. Our approach provides a unified treatment of several hitherto independent results, and gives new results for the category of partial transformations.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 5 , Issue 1 , August 1971 , pp. 75 - 86
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Munn, W.O., “Fundamental inverse semigroups”, Quart. J. Math. Oxford (2) 21 (1970), 157–170.CrossRefGoogle Scholar
[2]Preston, G.B., “Embedding any semigroup in a D-simple semigroup”, Trans. Amer. Math. Soc. 93 (1959), 351–355.Google Scholar
[3]Reilly, N.R., “Embedding inverse semigroups in bisimple inverse semigroups”, Quart. J. Math. Oxford (2) 16 (1965), 183–187.CrossRefGoogle Scholar
[4]Zareckiĭ, K.A., “The semigroup of binary relations” (Russian), Mat. Sb. (N.S.) 61 (103) (1963), 291–305.Google Scholar