Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T19:01:48.323Z Has data issue: false hasContentIssue false
  • English
  • Français

DISCRETENESS CRITERIA FOR MÖBIUS GROUPS ACTING ON II

Published online by Cambridge University Press:  19 June 2009

LIU-LAN LI  and
XIAN-TAO WANG
LIU-LAN LI
Affiliation:
Department of Mathematics, Hengyang Normal University, Hengyang, Hunan 421008, P.R. China (email: [email protected])
XIAN-TAO WANG*
Affiliation:
Department of Mathematics, Hunan Normal University Changsha, Hunan 410081, P.R. China (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Jørgensen’s famous inequality gives a necessary condition for a subgroup of PSL(2,ℂ) to be discrete. It is also true that if Jørgensen’s inequality holds for every nonelementary two-generator subgroup, the group is discrete. The sufficient condition has been generalized to many settings. In this paper, we continue the work of Wang, Li and Cao (‘Discreteness criteria for Möbius groups acting on 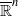’, Israel J. Math.150 (2005), 357–368) and find three more (infinite) discreteness criteria for groups acting on 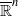; we also correct a linguistic ambiguity of their Theorem 3.3 where one of the necessary conditions might be vacuously fulfilled. The results of this paper are obtained by using known results regarding two-generator subgroups and a careful analysis of the relation among the fixed point sets of various elements of the group.

Keywords

discreteness criteriontwo-generator Möbius groupparabolic elementloxodromic elementg-elliptic element
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 80 , Issue 2 , October 2009 , pp. 275 - 290
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2009

Footnotes

This research was partially supported by the Program for NCET (No. 04-0783), NSF of China (No. 10771059) and Hengyang Normal University (No. 08B06).

References

[1] Abikoff, W. and Haas, A., ‘Nondiscrete groups of hyperbolic motions’, Bull. London Math. Soc. 22 (1990), 233–238.CrossRefGoogle Scholar
[2] Ahlfors, L. V., ‘On the fixed points of Möbius transformations in ’, Ann. Acad. Sci. Fenn. Ser. A I Math. 10 (1985), 15–27.CrossRefGoogle Scholar
[3] Baribeau, L. and Ransford, T., ‘On the set of discrete two-generator groups’, Math. Proc. Cambridge Philos. Soc. 128 (2000), 245–255.CrossRefGoogle Scholar
[4] Beardon, A. F., The Geometry of Discrete Groups, Graduate Text in Mathematics, 91 (Springer, Berlin, 1983).CrossRefGoogle Scholar
[5] Beardon, A. F., ‘Some remarks on nondiscrete Möbius groups’, Ann. Acad. Sci. Fenn. Ser. A I Math. 21 (1996), 69–79.Google Scholar
[6] Chen, M., ‘Discreteness and convergence of Möbius groups’, Geom. Dedicata 104 (2004), 61–69.CrossRefGoogle Scholar
[7] Chen, S. S. and Greenberg, L., Hyperbolic Spaces, Contributions to Analysis (Academic Press, New York, 1974), pp. 49–87.CrossRefGoogle Scholar
[8] Chu, Y. and Wang, X., ‘The discrete and nondiscrete subgroups of SL(2,ℝ) and SL(2,ℂ)’, Hokkaido Math. J. 30 (2001), 649–659.CrossRefGoogle Scholar
[9] Fang, A. and Nai, B., ‘On the discreteness and convergence in n-dimensional Möbius groups’, J. London Math. Soc. 61 (2000), 761–773.Google Scholar
[10] Gilman, J., ‘Inequalities in discrete subgroups of PSL(2,ℝ)’, Canad. J. Math. 40 (1988), 114–130.CrossRefGoogle Scholar
[11] Hersonsky, S., ‘A generalization of the Shimizu–Leutbecher and Jørgensen inequalities to Möbius transformations in ℝN’, Proc. Amer. Math. Soc. 121 (1994), 209–215.Google Scholar
[12] Isachenko, N. A., ‘Systems of generators of subgroups of PSL(2,ℝ)’, Siberian Math. J. 31 (1990), 162–165.CrossRefGoogle Scholar
[13] Jørgensen, T., ‘On discrete groups of Möbius transformations’, Amer. J. Math. 98 (1976), 739–749.CrossRefGoogle Scholar
[14] Jørgensen, T., ‘A note on subgroups of SL(2,ℂ)’, Quart. J. Math. Oxford 28 (1977), 209–212.CrossRefGoogle Scholar
[15] Martin, G.J., ‘On discrete Möbius groups in all dimensions’, Acta Math. 163 (1989), 253–289.CrossRefGoogle Scholar
[16] Sullivan, D., ‘Quasiconformal homeomorphisms and dynamics II: structural stability implies hyperbolicity for Kleinian groups’, Acta Math. 155 (1985), 243–260.CrossRefGoogle Scholar
[17] Tukia, P., ‘Differentiability and rigidity of Möbius groups’, Invent. Math. 82 (1985), 557–578.CrossRefGoogle Scholar
[18] Tukia, P. and Wang, X., ‘Discreteness of subgroups of SL(2,ℂ) containing elliptic elements’, Math. Scand. 91 (2002), 214–220.CrossRefGoogle Scholar
[19] Wang, X., ‘Dense subgroups of n-dimensional Möbius groups’, Math. Z. 243 (2003), 643–651.CrossRefGoogle Scholar
[20] Wang, X., ‘Algebraic convergence theorems of n-dimensional Kleinian groups’, Israel J. Math. 162 (2007), 221–233.CrossRefGoogle Scholar
[21] Wang, X., Li, L. and Cao, W., ‘Discreteness criteria for Möbius groups acting on ’, Israel J. Math. 150 (2005), 357–368.CrossRefGoogle Scholar
[22] Wang, X. and Yang, W., ‘Discreteness criteria of Möbius groups of high dimensions and convergence theorem of Kleinian groups’, Adv. Math. 159 (2001), 68–82.CrossRefGoogle Scholar
[23] Wang, X. and Yang, W., ‘Discreteness criteria for subgroups in SL(2,ℂ)’, Math. Proc. Cambridge Philos. Soc. 124 (1998), 51–55.CrossRefGoogle Scholar
[24] Wang, X. and Yang, W., ‘Dense subgroups and discrete subgroups in SL(2,ℂ)’, Quart. J. Math. Oxford 50 (1999), 517–521.CrossRefGoogle Scholar
[25] Wang, X. and Yang, W., ‘Generating systems of subgroups in PSL(2,Γn)’, Proc. Edinburgh Math. Soc. 45 (2002), 49–58.CrossRefGoogle Scholar
[26] Wang, S. C. and Zhou, Q., ‘On the proper conjugation of Kleinian groups’, Geom. Dedicata 50 (1995), 1–10.Google Scholar
[27] Waterman, P. L., ‘Möbius transformations in several dimensions’, Adv. Math. 101 (1993), 87–113.CrossRefGoogle Scholar
[28] Waterman, P. L., ‘Purely elliptic Möbius groups’, in: Holomorphic Functions and Moduli, Vol. II (Berkeley, CA, 1986), Mathematical Sciences Research Institute Publications, 11 (Springer, New York, 1988), pp. 173–178.Google Scholar
[29] Wielenberg, N. J., ‘Discrete Möbius groups: fundamental polyhedra and convergence’, Amer. J. Math. 99 (1977), 861–877.CrossRefGoogle Scholar
[30] Yang, S., ‘On the discreteness in SL(2,ℂ)’, Math. Z. 255 (2007), 227–230.CrossRefGoogle Scholar