Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T02:16:01.225Z Has data issue: false hasContentIssue false
  • English
  • Français

DISCRETENESS CRITERIA FOR ISOMETRIC GROUPS ACTING ON COMPLEX HYPERBOLIC SPACES

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  17 March 2010

XI FU
XI FU*
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha, Hunan 410081, PR China (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, four new discreteness criteria for isometric groups on complex hyperbolic spaces are proved, one of which shows that the Condition C hypothesis in Cao [‘Discrete and dense subgroups acting on complex hyperbolic space’, Bull. Aust. Math. Soc.78 (2008), 211–224, Theorem 1.4] is removable; another shows that the parabolic condition hypothesis in Li and Wang [‘Discreteness criteria for Möbius groups acting on 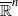II’, Bull. Aust. Math. Soc.80 (2009), 275–290, Theorem 3.1] is not necessary.

Keywords

discreteness criterianonelementarycomplex hyperbolic spacesloxodromic

MSC classification

Secondary: 20F67: Hyperbolic groups and nonpositively curved groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 81 , Issue 3 , June 2010 , pp. 481 - 487
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Basmajian, A. and Miner, R., ‘Discrete groups of complex hyperbolic motion’, Invent. Math. 131 (1998), 85–136.CrossRefGoogle Scholar
[2]Cao, W., ‘Discrete and dense subgroups acting on complex hyperbolic space’, Bull. Aust. Math. Soc. 78 (2008), 211–224.CrossRefGoogle Scholar
[3]Cao, W. and Wang, X., ‘Discreteness criteria and algebraic convergence theorem for subgroups in PU (1,n;ℂ)’, Proc. Japan Acad. 82 (2006), 49–52.Google Scholar
[4]Chen, S. S. and Greenberg, L., Hyperbolic Spaces: Constributions to Analysis (Academic Press, New York, 1974), pp. 49–87.Google Scholar
[5]Dai, B., Fang, A. and Nai, B., ‘Discreteness criteria for subgroups in complex hyperbolic space’, Proc. Japan Acad. 77 (2001), 168–172.Google Scholar
[6]Goldman, W. M., Complex Hyperbolic Geometry (Oxford University Press, New York, 1999).CrossRefGoogle Scholar
[7]Jørgensen, T., ‘On discrete groups of Möbius transformation’, Amer. J. Math. 98 (1976), 739–749.CrossRefGoogle Scholar
[8]Kamiya, S., ‘Notes on elements of U(1,n:ℂ)’, Hiroshima Math. J. 21 (1991), 23–45.Google Scholar
[9]Kamiya, S., ‘Chordal and matrix norms of unitary transformations’, First Korean–Japanese Colloquium on Finite or Infinite Dimensional Complex Analysis (1993), 121–125.Google Scholar
[10]Li, L. and Wang, X., ‘Discreteness criteria for Möbius groups acting on II’, Bull. Aust. Math. Soc. 80 (2009), 275–290.CrossRefGoogle Scholar
[11]Parker, J. R., ‘Uniform discreteness and Heisenberg transformation’, Math. Z. 225 (1997), 485–505.CrossRefGoogle Scholar
[12]Tukia, P. and Wang, X., ‘Discreteness of subgroup of SL(2,ℂ) containing elliptic elements’, Math. Scand. 91 (2004), 214–220.CrossRefGoogle Scholar
[13]Wang, X., ‘Dense subgroups of n-dimensional Möbius groups’, Math. Z. 243 (2003), 643–651.CrossRefGoogle Scholar
[14]Wang, X., Li, L. and Cao, W., ‘Discreteness criteria for Möbius groups acting on ’, Israel J. Math. 150 (2005), 357–368.CrossRefGoogle Scholar
[15]Yang, S., ‘On the discreteness in SL(2,ℂ)’, Math. Z. 255 (2007), 227–230.CrossRefGoogle Scholar
[16]Yang, S., ‘Discreteness criteria for isometric groups of real and complex hyperbolic space’, Indiana Univ. Math. J. 58 (2009), 1443–1456.CrossRefGoogle Scholar