Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T02:41:51.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete quadratic estimates and holomorphic functional calculi in Banach spaces

Published online by Cambridge University Press:  17 April 2009

Edwin Franks  and
Alan McIntosh
Edwin Franks
Affiliation:
Department of Mathematics, Macquarie University, New South Wales 2109, Australia, e-mail: [email protected], [email protected]
Alan McIntosh
Affiliation:
Department of Mathematics, Macquarie University, New South Wales 2109, Australia, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop a discrete version of the weak quadratic estimates for operators of type w explained by Cowling, Doust, McIntosh and Yagi, and show that analogous theorems hold. The method is direct and can be generalised to the case of finding necessary and sufficient conditions for an operator T to have a bounded functional calculus on a domain which touches σ(T) nontangentially at several points. For operators on Lp, 1 < p < ∞, it follows that T has a bounded functional calculus if and only if T satisfies discrete quadratic estimates. Using this, one easily obtains Albrecht's extension to a joint functional calculus for several commuting operators. In Hilbert space the methods show that an operator with a bounded functional calculus has a uniformly bounded matricial functional calculus.

The basic idea is to take a dyadic decomposition of the boundary of a sector Sv. Then on the kth ingerval consider an orthonormal sequence of polynomials 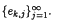. For h ∈ H∞(Sν), estimates for the uniform norm of h on a smaller sector Sμ are obtained from the coefficients akj = (h, ek, j). These estimates are then used to prove the theorems.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 58 , Issue 2 , October 1998 , pp. 271 - 290
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Albrecht, D., Functional calculi of commuting unbounded operators, Ph.D. thesis (Monash University, Melbourne, Australia, 1994).Google Scholar
[2]Albrecht, D., Duong, X.T. and McIntosh, A., ‘Operator theory and harmonic analysis’, in Workshop on Analysis and Geometry, 1995, Part III, Proceedings of the Centre for Mathematics and its Applications 34 (C.M.A., A.N.U., Canberra, Australia, 1996), pp. 77–136.Google Scholar
[3]Albrecht, D., Franks, E. and McIntosh, A., Holomorphic functional calculi and sums of commuting operators (Macquarie University Mathematics Report, 1998).Google Scholar
[4]Auscher, P., McIntosh, A. and Nahmod, A., ‘Holomorphic functional calculi of operators, quadratic estimates and interpolation’, Indiana Univ. Math. J. 46 (1997), 375–403.CrossRefGoogle Scholar
[5]Boyadzhiev, K. and de Laubenfels, R., ‘Semigroups and resolvents of bounded variation, imaginary powers and H ∞ functional calculus’, Semigroup Forum 45 (1992), 372–384.CrossRefGoogle Scholar
[6]Cowling, M., Doust, I., McIntosh, A. and Yagi, A., ‘Banach space operators with a bounded H ∞ functional calculus’, J. Austral. Math. Soc. Ser. A 60 (1996), 51–89.CrossRefGoogle Scholar
[7]Franks, E., ‘Polynomially subnormal operator tuples’, J. Operator Theory 31 (1994), 219–228.Google Scholar
[8]Franks, E., ‘Modified Cauchy kernels and functional calculus for operators on Banach space’, J. Austral. Math. Soc. Ser. A 63 (1997), 91–99.CrossRefGoogle Scholar
[9]Franks, E., ‘A new approach to quadratic estimates, functional calculus, and similarity for type ω operators on Hilbert spaces’, (in preparation).Google Scholar
[10]Lancien, F., Lancien, G. and Le Merdy, C., ‘A joint functional calculus for sectorial operators with commuting resolvents’, Proc. London Math. Soc. (to appear).Google Scholar
[11]Lancien, G. and Le Merdy, C, ‘A generalized H ∞ functional calculus for operators on subspaces of L p and application to maximal regularity’, (preprint).Google Scholar
[12]McIntosh, A. and Yagi, A., ‘Operators of type-ω without a bounded H ∞ functional calculus’, in Miniconference on Operators in Analysis, Proc. Centre. Math. Analysis 24 (A.N.U., Canberra, Australia, 1989), pp. 159–172.Google Scholar
[13]McIntosh, A., ‘Operators which have an H ∞ functional calculus’, in Miniconference on Operator Theory and Partial Differential Equations, Proc. Centre Math. Analysis 14 (A.N.U., Canberra, Australia, 1986), pp. 210–231.Google Scholar
[14]Le Merdy, C., ‘The similarity problem for bounded analytic semigroups on Hilbert space’, Semigroup Forum 56 (1998), 205–224.CrossRefGoogle Scholar
[15]Paulsen, V.I., ‘Every completely polynomially bounded operator is similar to a contraction’, J. Funct. Anal. 55 (1984), 1–17.CrossRefGoogle Scholar
[16]Stein, E.M., Singular Integrals and Differentiability Properties of Functions (Princeton University Press, Princeton, New Jersey, 1970).Google Scholar