Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-05T20:41:54.991Z Has data issue: false hasContentIssue false
  • English
  • Français

DIGITALLY RESTRICTED SETS AND THE GOLDBACH CONJECTURE

Part of: Additive number theory; partitions Elementary number theory

Published online by Cambridge University Press:  04 February 2025

JAMES CUMBERBATCH Open the ORCID record for JAMES CUMBERBATCH [Opens in a new window]
JAMES CUMBERBATCH*
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for any set D of at least two digits in a given base b, almost all even integers taking digits only in D when written in base b satisfy the Goldbach conjecture. More formally, if 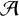$\mathcal {A}$ is the set of numbers whose digits base b are exclusively from D, almost all elements of 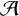$\mathcal {A}$ satisfy the Goldbach conjecture. Moreover, the number of even integers in 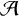$\mathcal {A}$ which are less than X and not representable as the sum of two primes is less than 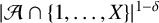$|\mathcal {A}\cap \{1,\ldots ,X\}|^{1-\delta }$.

Keywords

Goldbachdigitsexceptional setsdigitally restricted sets

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes
Secondary: 11A63: Radix representation; digital problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author’s work is supported by NSF grant DMS-2001549.

References

Brüdern, J., Kawada, K. and Wooley, T. D., ‘Additive representation in thin sequences, II: The binary Goldbach problem’, Mathematika 47(1–2) (2000), 117–125.CrossRefGoogle Scholar
Chudakov, N. G., ‘Sur le problème de Goldbach’, C. R. (Dokl.) Acad. Sci. URSS, n. Ser. 17 (1937), 335–338.Google Scholar
Estermann, T., ‘On Goldbach’s problem: proof that almost all even positive integers are sums of two primes’, Proc. Lond. Math. Soc. (2) 44(1) (1938), 307–314.CrossRefGoogle Scholar
Heilbronn, H., ‘Review of I. M. Vinogradov, “Representation of an odd number as a sum of three primes”’, Z. Math. 16 (1937), 291–292.Google Scholar
Konyagin, S., ‘Arithmetic properties of integers with missing digits: distribution in residue classes’, Period. Math. Hungar. 42(1–2) (2001), 145–162.CrossRefGoogle Scholar
Mauduit, C. and Rivat, J., ‘Sur un problème de Gelfond: la somme des chiffres des nombres premiers’, Ann. of Math. (2) 171 (2010), 1591–1646.CrossRefGoogle Scholar
Maynard, J., ‘Primes with restricted digits’, Invent. Math. 217(1) (2019), 127–218.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., ‘The exceptional set of Goldbach’s problem’, Acta Arith. 27 (1975), 353–370.CrossRefGoogle Scholar
Perelli, A., ‘Goldbach numbers represented by polynomials’, Rev. Mat. Iberoam. 12(2) (1996), 477–490.CrossRefGoogle Scholar
Pintz, J., ‘A new explicit formula in the additive theory of primes with applications II. The exceptional set in Goldbach’s problem’, Preprint, 2018, arXiv:1804.09084.Google Scholar
van der Corput, J., ‘Sur l’hypothèse de Goldbach pour presque tous les nombres pairs’, Acta Arith. 2(2) (1936), 266–290.CrossRefGoogle Scholar
Vaughan, R. C., ‘Sommes trigonométriques sur les nombres premiers’, C. R. Acad. Sci. Paris Sér. A-B 285(16) (1977), 981–983.Google Scholar
Vinogradov, I. M., ‘Representation of an odd number as a sum of three primes’, C. R. (Dokl.) Acad. Sci. URSS, n. Ser. 15 (1937), 169–172.Google Scholar