Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Van Hove, Michel A.
Weinberg, William H.
and
Chan, Chi-Ming
1986.
Low-Energy Electron Diffraction.
Vol. 6,
Issue. ,
p.
467.
Khan, Adnan
Kalim, Muhammad
Akgül, Ali
Jarad, Fahd
and
Malik, Sarfraz Nawaz
2022.
The Extended Laguerre Polynomials
A
q
,
n
α
x
Involving
F
q
q
,
q
>
2
.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.
Khan, Adnan
Mateen, M. Haris
Akgül, Ali
Ali, Md. Shajib
and
Tul Ain, Qura
2022.
The
K
Extended Laguerre Polynomials Involving
A
α
r
,
n
,
k
x
F
r
r
,
r
>
2
.
Advances in Mathematical Physics,
Vol. 2022,
Issue. ,
p.
1.


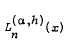 in powers of
in powers of 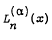 , have been defined by a Rodrigues type formula involving the forward difference operator Δ
, have been defined by a Rodrigues type formula involving the forward difference operator Δ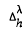 of Δ
of Δ