Published online by Cambridge University Press: 09 September 2015
The main goal is to illustrate that the so-called indirect function of a cooperative game in characteristic function form is applicable to determine the nucleolus for a subclass of coalitional games called compromise stable transferable utility (TU) games. In accordance with the Fenchel–Moreau theory on conjugate functions, the indirect function is known as the dual representation of the characteristic function of the coalitional game. The key feature of a compromise stable TU game is the coincidence of its core with a box prescribed by certain upper and lower core bounds. For the purpose of the determination of the nucleolus, we benefit from the interrelationship between the indirect function and the prekernel of coalitional TU games. The class of compromise stable TU games contains the subclasses of clan games, big boss games and 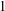 $1$- and
$1$- and 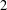 $2$-convex
$2$-convex  $n$-person TU games. As an adjunct, this paper reports the indirect function of clan games for the purpose of determining their nucleolus.
$n$-person TU games. As an adjunct, this paper reports the indirect function of clan games for the purpose of determining their nucleolus.