Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T02:30:40.507Z Has data issue: false hasContentIssue false
  • English
  • Français

DENSITY, SMITAL PROPERTY AND QUASICONTINUITY

Part of: Classical measure theory Topological and differentiable algebraic systems

Published online by Cambridge University Press:  04 December 2017

GRAŻYNA HORBACZEWSKA Open the ORCID record for GRAŻYNA HORBACZEWSKA [Opens in a new window]  and
SEBASTIAN LINDNER
GRAŻYNA HORBACZEWSKA*
Affiliation:
Department of Mathematics and Computer Science, University of Lodz, Banacha 22, 90 238 Lodz, Poland email [email protected]
SEBASTIAN LINDNER
Affiliation:
Department of Mathematics and Computer Science, University of Lodz, Banacha 22, 90 238 Lodz, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Based on the abstract version of the Smital property, we introduce an operator 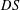$DS$. We use it to characterise the class of semitopological abelian groups, for which addition is a quasicontinuous operation.

Keywords

quasicontinuitySmital lemmasemitopological groups

MSC classification

Primary: 22A30: Other topological algebraic systems and their representations
Secondary: 28A05: Classes of sets (Borel fields, $sigma$-rings, etc.), measurable sets, Suslin sets, analytic sets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 246 - 252
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Balcerzak, M., Bartoszewicz, A., Rzepecka, J. and Wroñski, S., ‘On Marczewski fields and ideals’, Real Anal. Exchange 26(2) (2000–2001), 703–715.CrossRefGoogle Scholar
Bartoszewicz, A., Filipczak, M. and Natkaniec, T., ‘On Smital properties’, Topology Appl. 158 (2011), 2066–2075.CrossRefGoogle Scholar
Filipczak, M., Filipczak, T. and Knapik, R., ‘On Steinhaus and Smital properties for sets’, in preparation.Google Scholar
Horbaczewska, G. and Lindner, S., ‘Resolvability of measurable spaces’, Bull. Aust. Math. Soc. 94(1) (2016), 70–79.CrossRefGoogle Scholar
Illanes, A., ‘Finite and 𝜔-resolvability’, Proc. Amer. Math. Soc. 124 (1996), 1243–1246.Google Scholar
Jiménez, R. and Malykhin, V. I., ‘Structure resolvability’, Comment. Math. Univ. Carolin. 39(2) (1998), 379–387.Google Scholar
Kempisty, S., ‘Sur les fonctions quasicontinues’, Fund. Math. 19 (1932), 184–197.Google Scholar
Nowik, A., ‘Marczewski–Burstin representations vs. Bernstein and dense subsets’, Demonstratio Math. 49(4) (2016), 372–377.Google Scholar