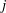Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-03-28T16:56:51.386Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DENSITY OF $j$-WISE RELATIVELY $r$-PRIME ALGEBRAIC INTEGERS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  06 July 2018

BRIAN D. SITTINGER Open the ORCID record for BRIAN D. SITTINGER [Opens in a new window]
BRIAN D. SITTINGER*
Affiliation:
CSU Channel Islands, 1 University Drive, Camarillo, CA 93012, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 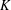$K$ be a number field with a ring of integers 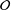${\mathcal{O}}$. We follow Ferraguti and Micheli [‘On the Mertens–Cèsaro theorem for number fields’, Bull. Aust. Math. Soc.93(2) (2016), 199–210] to define a density for subsets of 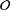${\mathcal{O}}$ and use it to find the density of the set of 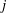$j$-wise relatively $r$-prime 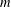$m$-tuples of algebraic integers. This provides a generalisation and analogue for several results on natural densities of integers and ideals of algebraic integers.

Keywords

number fieldsalgebraic integersnatural densityzeta function

MSC classification

Primary: 11R45: Density theorems
Secondary: 11R04: Algebraic numbers; rings of algebraic integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 221 - 229
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Benkoski, S. J., ‘The probability that k positive integers are relatively r-prime’, J. Number Theory 8 (1976), 218–223.Google Scholar
DeMoss, R. D. and Sittinger, B. D., ‘The probability that $k$ ideals in a ring of algebraic integers are $m$ -wise relatively prime’, Preprint, 2018, arXiv:1803.09187.Google Scholar
Ferraguti, A. and Micheli, G., ‘On the Mertens–Cèsaro theorem for number fields’, Bull. Aust. Math. Soc. 93(2) (2016), 199–210.Google Scholar
Gegenbauer, L., ‘Asymptotische Gesetze der Zahlentheorie’, Denkshcriften Akad. Wien 9 (1885), 37–80.Google Scholar
Hu, J., ‘The probability that random positive integers are k-wise relatively prime’, Int. J. Number Theory 9 (2013), 1263–1271.Google Scholar
Lehmer, D. N., ‘Asymptotic evaluation of certain totient sums’, Amer. J. Math. 22 (1900), 293–335.Google Scholar
Mertens, F., ‘Über einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338.Google Scholar
Sittinger, B. D., ‘The probability that random algebraic integers are relatively r-prime’, J. Number Theory 130 (2010), 164–171.Google Scholar
Tóth, L., ‘The probability that k positive integers are pairwise relatively prime’, Fibonacci Quart. 40 (2002), 13–18.Google Scholar