Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-26T09:11:45.986Z Has data issue: false hasContentIssue false
  • English
  • Français

DENSE SETS OF INTEGERS WITH A PRESCRIBED REPRESENTATION FUNCTION

Part of: Sequences and sets

Published online by Cambridge University Press:  16 June 2011

MIN TANG
MIN TANG*
Affiliation:
Department of Mathematics, Anhui Normal University, Wuhu 241000, PR China (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A set A⊆ℤ is called an asymptotic basis of ℤ if all but finitely many integers can be represented as a sum of two elements of A. Let A be an asymptotic basis of integers with prescribed representation function, then how dense A can be? In this paper, we prove that there exist a real number c>0 and an asymptotic basis A with prescribed representation function such that 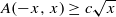for infinitely many positive integers x.

Keywords

prescribed representation functionSidon sets

MSC classification

Secondary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 84 , Issue 1 , August 2011 , pp. 40 - 43
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Chen, Y. G., ‘A problem on unique representation bases’, European J. Combin. 28 (2007), 33–35.CrossRefGoogle Scholar
[2]Cilleruelo, J. and Nathanson, M. B., ‘Perfect difference sets constructed from Sidon sets’, Combinatorica 28 (2008), 401–414.CrossRefGoogle Scholar
[3]Cilleruelo, J. and Nathanson, M. B., ‘Dense sets of integers with prescribed representation functions’, Preprint, 2007.Google Scholar
[4]Lee, J., ‘Infinitely often dense bases for the integers with a prescribed representation function’, Integers 10 (2010), 299–307.CrossRefGoogle Scholar
[5]Nathanson, M. B., ‘Unique representation bases for integers’, Acta Arith. 108 (2003), 1–8.CrossRefGoogle Scholar
[6]Nathanson, M. B., ‘Every function is the representation function of an additive basis for the integers’, Port. Math. 62 (2005), 55–72.Google Scholar