Published online by Cambridge University Press: 17 April 2009
For a knot K in a homology 3-sphere Σ, by Σ(K;p/q), we denote the resulting 3-manifold of p/q-surgery along K. We say that the manifold or the surgery is of lens type if Σ(K;p/q) has the same Reidemeister torsion as a lens space.
We prove that, for Σ(K;p/q) to be of lens type, it is a necessary and sufficient condition that the Alexander polynomial ΔK(t) of K is equal to that of an (i, j)-torus knot T(i, j) modulo (tp – 1).
We also deduce two results: If Σ(K;p/q) has the same Reidemeister torsion as L(p, q') then
(1) 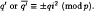 (2) The multiple of ΣK(tk) over k ∈ (i) is ±tm modulo (tp – 1), where (i) is the subgroup in (Z/pZ)×/{±1} generated by i. Conversely, if a subgroup H of (Z/pZ)×/{±l} satisfying that the product of ΣK(tk) (k ∈ H) is ±tm modulo (tp – 1), then H includes i or j.
(2) The multiple of ΣK(tk) over k ∈ (i) is ±tm modulo (tp – 1), where (i) is the subgroup in (Z/pZ)×/{±1} generated by i. Conversely, if a subgroup H of (Z/pZ)×/{±l} satisfying that the product of ΣK(tk) (k ∈ H) is ±tm modulo (tp – 1), then H includes i or j.
Here, i, j are the parameters of the torus knot above.