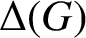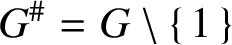Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ma, Xuanlong
and
Zhai, Liangliang
2021.
Strong metric dimensions for power graphs of finite groups.
Communications in Algebra,
Vol. 49,
Issue. 11,
p.
4577.
Bera, Sudip
and
Dey, Hiranya Kishore
2022.
On the proper enhanced power graphs of finite nilpotent groups.
Journal of Group Theory,
Vol. 0,
Issue. 0,
BEIKE, NICOLAS F.
CARLETON, RACHEL
COSTANZO, DAVID G.
HEATH, COLIN
LEWIS, MARK L.
LU, KAIWEN
and
PEARCE, JAMIE D.
2022.
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 105,
Issue. 1,
p.
92.
Bera, S.
2024.
On the strong domination number of proper enhanced power graphs of finite groups.
Acta Mathematica Hungarica,
Vol. 174,
Issue. 1,
p.
177.
LEWIS, MARK L.
and
MONETTA, CARMINE
2024.
ON NEIGHBOURHOODS IN THE ENHANCED POWER GRAPH ASSOCIATED WITH A FINITE GROUP.
Bulletin of the Australian Mathematical Society,
p.
1.
Kumar, Jitender
Panda, Ramesh Prasad
and
Parveen
2024.
On the difference graph of power graphs of finite groups.
Quaestiones Mathematicae,
Vol. 47,
Issue. 5,
p.
997.
Ma, Xuanlong
Zahirović, Samir
Lv, Yubo
and
She, Yanhong
2024.
Forbidden subgraphs in enhanced power graphs of finite groups.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 3,
Mohamed, Norlyda
Ali, Nor Muhainiah Mohd
and
Bello, Muhammed
2024.
On the deep enhanced power graph of dihedral group.
Vol. 3080,
Issue. ,
p.
080014.
Mohamed, Norlyda
Ali, Nor Muhainiah Mohd
and
Bello, Muhammed
2024.
Properties of deep enhanced power graphs of semi-dihedral groups.
Vol. 3203,
Issue. ,
p.
110010.