Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T11:35:07.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The curvature and topological properties of hypersurfaces with constant scalar curvature

Published online by Cambridge University Press:  17 April 2009

Shu Shichang  and
Liu Sanyang
Shu Shichang
Affiliation:
Department of Applied Mathematics, Xidian University, Xi'an 710071, Shaanxi, Peoples Republic of China, e-mail: [email protected]
Liu Sanyang
Affiliation:
Department of Mathematics, Xianyang Teachers' University, Xianyang 712000, Shaanxi, Peoples Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider n (n ≥ 3)-dimensional compact oriented connected hypersurfaces with constant scalar curvature n(n − 1)r in the unit sphere Sn+1(1). We prove that, if r ≥ (n − 2)/(n − 1) and S ≤ (n − 1)(n(r − 1) + 2)/(n − 2) + (n − 2)/(n(r − 1) + 2), then either M is diffeomorphic to a spherical space form if n = 3; or M is homeomorphic to a sphere if n ≥ 4; or M is isometric to the Riemannian product 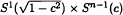, where c2 = (n − 2)/(nr) and S is the squared norm of the second fundamental form of M.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 70 , Issue 1 , August 2004 , pp. 35 - 44
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Alencar, H. and do Carmo, M.P., ‘Hypersurfaces with constant mean curvature in spheres’, Proc. Amer. Math. Soc. 120 (1994), 1223–1229.CrossRefGoogle Scholar
[2]Aubin, T., Some nonlinear problems in Riemannian geometry (Springer-Verlag, Berlin, New York, 1998).CrossRefGoogle Scholar
[3]Cheng, S.Y. and Yau, S.T., ‘Hypersurfaces with constant scalar curvature’, Math. Ann. 225 (1997), 195–204.CrossRefGoogle Scholar
[4]Cheng, Q.M., ‘Hypersurfaces in a unit sphere S n+1(1)with constant scalar curvature’, J. London Math. Society 64 (2001), 755–768.CrossRefGoogle Scholar
[5]Cai, K.R., ‘Topology of certain closed submanifolds in a Euclidean space’, Chinese Ann. Math. Ser. A 8 (1987), 234–241.Google Scholar
[6]Hamilton, R., ‘Three manifolds with positive Ricci curvature’, J. Differential Geom. 17 (1982), 255–306.CrossRefGoogle Scholar
[7]Li, H., ‘Hypersurfaces with constant scalar curvature in space forms’, Math. Ann. 305 (1996), 665–672.Google Scholar
[8]Lawson, H. and Simons, J., ‘On stable currents and their application to global problems in real and complex geometry’, Ann. of Math. 98 (1973), 427–450.CrossRefGoogle Scholar
[9]Leung, P.F., ‘An estimate on the Ricci curvature of a submanifold and some applications’, Proc. Amer. Math. Soc. 114 (1992), 1051–1061.CrossRefGoogle Scholar
[10]Leung, P.F., ‘Minimal submanifolds in sphere’, Math. Z. 183 (1983), 75–86.CrossRefGoogle Scholar
[11]Okumura, M., ‘Hypersurfaces and a pinching problem on the second fundamental tensor’, Amer. J. Math. 96 (1974), 207–213.CrossRefGoogle Scholar
[12]Shiohama, K. and Xu, H., ‘The topological sphere theorem for complete submanifolds’, Compositio Math. 107 (1997), 221–232.CrossRefGoogle Scholar
[13]Sjerve, D., ‘Homology spheres which are covered by spheres’. J. London Math. Soc. (2) 6 (1973), 333–336.CrossRefGoogle Scholar