Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T06:17:44.565Z Has data issue: false hasContentIssue false
  • English
  • Français

A converse of Bernstein's inequality for locally compact groups

Published online by Cambridge University Press:  17 April 2009

Walter R. Bloom
Walter R. Bloom
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a Hausdorff locally compact abelian group, Γ its character group. We shall prove that, if S is a translation-invariant subspace of Lp (G) (p ∈ [1, ∞]),

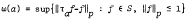
for each a ∈ G and 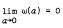, then 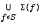is relatively compact (where Σ(f) denotes the spectrum of f). We also obtain a similar result when G is a Hausdorff compact (not necessarily abelian) group. These results can be considered as a converse of Bernstein's inequality for locally compact groups.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 9 , Issue 2 , October 1973 , pp. 291 - 298
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Bloom, Walter R., “Bernstein's inequality for locally compact abelian groups”, J. Austral. Math. Soc. (to appear).Google Scholar
[2]Edwards, D.A., “On translates of L ∞-functions”, J. London Math. Soc. 36 (1961), 431–432.CrossRefGoogle Scholar
[3]Edwards, R.E., “Translates of L ∞ functions and of bounded measures”, J. Austral. Math. Soc. 4 (1964), 403–409.CrossRefGoogle Scholar
[4]Edwards, R.E., Functional analysis: Theory and applications (Holt, Rinehart and Winston, New York, Chicago, San Francisco, Toronto, London, 1965).Google Scholar
[5]Edwards, R.E., Integration and harmonic analysis on compact groups (Notes on Pure Mathematics, 5. Australian National University, Canberra, 1970).Google Scholar
[6]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis. Volume I (Die Grundlehren der mathematischen Wissenschaften, Band 115. Academic Press, New York; Springer-Verlag, Berlin, Göttingen, Heidelberg; 1963).Google Scholar
[7]Reiter, Hans, Classical harmonic analysis and locally compact groups (Clarendon Press, Oxford, 1968).Google Scholar
[8]Rudin, Walter, Fourier analysis on groups (interscience, New York, London, 1962; 2nd Printing, 1967).Google Scholar