Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T02:13:08.640Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVERGENCE OF MANN’S ALTERNATING PROJECTIONS IN CAT($\unicode[STIX]{x1D705}$) SPACES

Part of: General theory of linear operators Global differential geometry Equations and inequalities involving nonlinear operators

Published online by Cambridge University Press:  03 May 2018

BYOUNG JIN CHOI Open the ORCID record for BYOUNG JIN CHOI [Opens in a new window]
BYOUNG JIN CHOI*
Affiliation:
Department of Mathematics, Institute for Industrial and Applied Mathematics, Chungbuk National University, Cheongju 28644, Korea email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the convex feasibility problem in 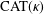$\text{CAT}(\unicode[STIX]{x1D705})$ spaces using Mann’s iterative projection method. To do this, we extend Mann’s projection method in normed spaces to 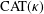$\text{CAT}(\unicode[STIX]{x1D705})$ spaces with 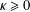$\unicode[STIX]{x1D705}\geq 0$, and then we prove the 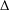$\unicode[STIX]{x1D6E5}$-convergence of the method. Furthermore, under certain regularity or compactness conditions on the convex closed sets, we prove the strong convergence of Mann’s alternating projection sequence in 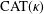$\text{CAT}(\unicode[STIX]{x1D705})$ spaces with 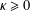$\unicode[STIX]{x1D705}\geq 0$.

Keywords

convex feasibility problemCAT(𝜅) space𝛥-convergenceMann’s alternating projection method

MSC classification

Primary: 47J25: Iterative procedures
Secondary: 47A46: Chains (nests) of projections or of invariant subspaces, integrals along chains, etc. 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 134 - 143
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Ariza-Ruiz, D., López-Acedo, G. and Nicolae, A., ‘The asymptotic behavior of the composition of firmly nonexpansive mappings’, J. Optim. Theory Appl. 167 (2015), 409–429.Google Scholar
Bačák, M., Searston, I. and Sims, B., ‘Alternating projections in CAT(0) spaces’, J. Math. Anal. Appl. 385 (2012), 599–607.Google Scholar
Bauschke, H. H. and Borwein, J. M., ‘On projection algorithms for solving convex feasibility problems’, SIAM Rev. 38 (1996), 367–426.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A., Metric Spaces of Non-positive Curvature, Fundamental Principles of Mathematical Sciences, 319 (Springer, Berlin, 1999).Google Scholar
Choi, B. J., Ji, U. C. and Lim, Y., ‘Convergences of alternating projections in CAT(𝜅) spaces’, Constr. Approx. (2017), to appear; doi: 10.1007/s00365-017-9382-6.Google Scholar
Choi, B. J., Ji, U. C. and Lim, Y., ‘Convex feasibility problems on uniformly convex metric spaces’, Preprint, 2017.CrossRefGoogle Scholar
Combettes, P. L., ‘Hilbertian convex feasibility problem: convergence of projection methods’, Appl. Math. Optim. 35 (1997), 311–330.Google Scholar
Dhompongsa, S. and Panyanak, B., ‘On 𝛥-convergence in CAT(0) spaces’, Comput. Math. Appl. 56 (2008), 2572–2579.Google Scholar
Espínola, R. and Fernández-León, A., ‘CAT(𝜅)-spaces, weak convergence and fixed points’, J. Math. Anal. Appl. 353 (2009), 410–427.CrossRefGoogle Scholar
He, J. S., Fang, D. H., López, G. and Li, C., ‘Mann’s algorithm for nonexpansive mappings in CAT(𝜅) spaces’, Nonlinear Anal. 75 (2012), 445–452.CrossRefGoogle Scholar
Ishikawa, S., ‘Fixed points and iteration of a nonexpansive mapping in a Banach space’, Proc. Amer. Math. Soc. 59 (1976), 65–71.Google Scholar
Kimura, Y., Saejung, S. and Yotkaew, P., ‘The Mann algorithm in a complete geodesic space with curvature bounded above’, Fixed Point Theory Appl. 2013 (2013), article ID 336.Google Scholar
Lim, T. C., ‘Remarks on some fixed point theorems’, Proc. Amer. Math. Soc. 60 (1976), 179–182.Google Scholar
Mann, W. R., ‘Mean value methods in iteration’, Proc. Amer. Math. Soc. 4 (1953), 506–510.Google Scholar
von Neumann, J., Functional Operators II: The Geometry of Orthogonal Spaces, Annals of Mathematics Studies, 22 (Princeton University Press, Princeton, NJ, 1950), reprint of mimeographed lecture notes first distributed in 1933.Google Scholar
Ohta, S., ‘Convexities of metric spaces’, Geom. Dedicata 125 (2007), 225–250.Google Scholar
Reich, S., ‘Weak convergence theorems for nonexpansive mappings in Banach spaces’, J. Math. Anal. Appl. 67 (1979), 274–276.Google Scholar
Sturm, K.-T., ‘Probability measures on metric spaces of nonpositive curvature’, in: Heat Kernels and Analysis on Manifolds, Graphs, and Metric Spaces, Contemporary Mathematics, 338 (American Mathematical Society, Providence, RI, 2003), 357–390.Google Scholar
Xu, H. K., ‘Iterative algorithms for nonlinear operators’, J. Lond. Math. Soc. 66 (2002), 240–256.Google Scholar