Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T13:15:45.851Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTRACTIBLE PERIODIC ORBITS OF LAGRANGIAN SYSTEMS

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Hamiltonian and Lagrangian mechanics

Published online by Cambridge University Press:  30 January 2019

MIGUEL PATERNAIN Open the ORCID record for MIGUEL PATERNAIN [Opens in a new window]
MIGUEL PATERNAIN*
Affiliation:
Universidad de la República, Centro de Matemática, Facultad de Ciencias, Iguá 4225, 11400 Montevideo, Uruguay email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a convex Lagrangian 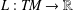$L:\mathit{TM}\rightarrow \mathbb{R}$ quadratic at infinity with 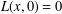$L(x,0)=0$ for every 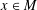$x\in M$ and such that the 1-form 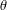$\unicode[STIX]{x1D703}$ defined by 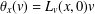$\unicode[STIX]{x1D703}_{x}(v)=L_{v}(x,0)v$ is not closed. We show that for every number 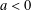$a<0$, there is a contractible (nonconstant) periodic orbit with action $a$. We also obtain estimates of the period and energy of such periodic orbits.

Keywords

convex Lagrangianaction functionalperiodic orbit

MSC classification

Primary: 37J45: Periodic, homoclinic and heteroclinic orbits; variational methods, degree-theoretic methods
Secondary: 70H12: Periodic and almost periodic solutions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 445 - 453
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The author was supported by an Anii grant.

References

Abbondandolo, A., ‘Lectures on the free period Lagrangian action functional’, J. Fixed Point Theory Appl. 13(2) (2013), 397–430.Google Scholar
Abbondandolo, A. and Schwarz, M., ‘A smooth pseudo-gradient for the Lagrangian action functional’, Adv. Nonlinear Stud. 9(4) (2009), 597–623.Google Scholar
Abraham, R. and Marsden, J. E., Foundations of Mechanics, 2nd edn (Addison-Wesley, Reading, MA, 1978), revised and enlarged with the assistance of Tudor Ratiu and Richard Cushman.Google Scholar
Bahri, A. and Taimanov, I. A., ‘Periodic orbits in magnetic fields and Ricci curvature of Lagrangian systems’, Trans. Amer. Math. Soc. 350(7) (1998), 2697–2717.Google Scholar
Benci, V., ‘Normal modes of a Lagrangian system constrained in a potential well’, Ann. Inst. H. Poincaré Anal. Non Linéaire 1(5) (1984), 379–400.Google Scholar
Benci, V., ‘Periodic solutions of Lagrangian systems on a compact manifold’, J. Differential Equations 63(2) (1986), 135–161.Google Scholar
Contreras, G., ‘The Palais–Smale condition on contact type energy levels for convex Lagrangian systems’, Calc. Var. Partial Differential Equations 27(3) (2006), 321–395.Google Scholar
Contreras, G., Delgado, J. and Iturriaga, R., ‘Lagrangian flows: the dynamics of globally minimizing orbits. II’, Bol. Soc. Brasil. Mat. (N.S.) 28(2) (1997), 155–196.Google Scholar
Contreras, G. and Iturriaga, R., Global Minimizers of Autonomous Lagrangians, 22nd Brazilian Mathematics Colloq. (Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 1999).Google Scholar
Contreras, G., Iturriaga, R., Paternain, G. P. and Paternain, M., ‘The Palais–Smale condition and Mañé’s critical values’, Ann. Inst. Henri Poincaré 1(4) (2000), 655–684.Google Scholar
Contreras, G., Macarini, L. and Paternain, G. P., ‘Periodic orbits for exact magnetic flows on surfaces’, Int. Math. Res. Not. IMRN 2004(8) (2004), 361–387.Google Scholar
Hofer, H. and Zehnder, E., Symplectic Invariants and Hamiltonian Dynamics, Modern Birkhäuser Classics (Birkhäuser, Basel, 1994).Google Scholar
Merry, W. J., ‘Closed orbits of a charge in a weakly exact magnetic field’, Pacific J. Math. 247(1) (2010), 189–212.Google Scholar
Novikov, S. P., ‘The Hamiltonian formalism and a multivalued analogue of Morse theory’, Uspekhi Mat. Nauk 37(5) (1982), 3–49, 248.Google Scholar
Palais, R. S., ‘Morse theory on Hilbert manifolds’, Topology 2 (1963), 299–340.Google Scholar
Paternain, M., ‘Periodic orbits with prescribed abbreviated action’, Proc. Amer. Math. Soc. 143(9) (2015), 4001–4008.Google Scholar
Paternain, M., ‘Periodic orbits of Lagrangian systems with prescribed action or period’, Proc. Amer. Math. Soc. 144(7) (2016), 2999–3007.Google Scholar
Struwe, M., Variational Methods: Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete, 34 (Springer, Berlin, 1996).Google Scholar
Taĭmanov, I. A., ‘Closed extremals on two-dimensional manifolds’, Uspekhi Mat. Nauk 47(2) (1992), 143–185, 223.Google Scholar