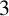1 Introduction
In an unpublished work, William Thurston defined a graph consisting of a vertex
![]() $v_{M}$
for every diffeomorphism type of a closed, orientable
$v_{M}$
for every diffeomorphism type of a closed, orientable
![]() $3$
-manifold M. Two vertices,
$3$
-manifold M. Two vertices,
![]() $v_{M}$
and
$v_{M}$
and
![]() $v_{M^{\prime }}$
, are connected by an edge if there exists a Dehn surgery between M and
$v_{M^{\prime }}$
, are connected by an edge if there exists a Dehn surgery between M and
![]() $M^{\prime }$
. In [Reference Hoffman and Walsh21], this graph is called the big Dehn surgery graph and studied in various ways.
$M^{\prime }$
. In [Reference Hoffman and Walsh21], this graph is called the big Dehn surgery graph and studied in various ways.
We define a directed graph encoding the structure of contact
![]() $(\pm 1)$
-surgeries on contact
$(\pm 1)$
-surgeries on contact
![]() $3$
-manifolds. The contact surgery graph
$3$
-manifolds. The contact surgery graph
![]() $\Gamma $
is the graph consisting of a vertex
$\Gamma $
is the graph consisting of a vertex
![]() $v_{(M,\xi )}$
for every contactomorphism type of a contact
$v_{(M,\xi )}$
for every contactomorphism type of a contact
![]() $3$
-manifold
$3$
-manifold
![]() $(M,\xi )$
. Whenever there exists a Legendrian knot L in
$(M,\xi )$
. Whenever there exists a Legendrian knot L in
![]() $(M_{1},\xi _{1})$
such that contact
$(M_{1},\xi _{1})$
such that contact
![]() $(-1)$
-surgery along L yields
$(-1)$
-surgery along L yields
![]() $(M_{2},\xi _{2})$
, we introduce a directed edge pointing from
$(M_{2},\xi _{2})$
, we introduce a directed edge pointing from
![]() $v_{(M_{1},\xi _{1})}$
to
$v_{(M_{1},\xi _{1})}$
to
![]() $v_{(M_{2},\xi _{2})}$
.
$v_{(M_{2},\xi _{2})}$
.
The contact surgery graph is closely tied to the properties of Stein or Weinstein cobordisms and fillings of contact manifolds since contact
![]() $(-1)$
-surgery along a Legendrian knot in a contact
$(-1)$
-surgery along a Legendrian knot in a contact
![]() $3$
-manifold
$3$
-manifold
![]() $(M,\xi )$
, also known as Legendrian surgery, corresponds to the attachment of a Weinstein
$(M,\xi )$
, also known as Legendrian surgery, corresponds to the attachment of a Weinstein
![]() $2$
-handle to the symplectisation of
$2$
-handle to the symplectisation of
![]() $(M,\xi )$
. The inverse operation of a contact
$(M,\xi )$
. The inverse operation of a contact
![]() $(-1)$
-surgery is called contact
$(-1)$
-surgery is called contact
![]() $(+1)$
-surgery.
$(+1)$
-surgery.
1.1 Properties of the contact surgery graph
In Section 2, we study the basic properties of
![]() $\Gamma $
. First, we observe that the contact surgery graph
$\Gamma $
. First, we observe that the contact surgery graph
![]() $\Gamma $
is connected by the work of Ding–Geiges [Reference Ding and Geiges4] who showed that any contact
$\Gamma $
is connected by the work of Ding–Geiges [Reference Ding and Geiges4] who showed that any contact
![]() $3$
-manifold can be constructed from the standard tight contact structure
$3$
-manifold can be constructed from the standard tight contact structure
![]() $\xi _{\mathrm {st}}$
on
$\xi _{\mathrm {st}}$
on
![]() $S^{3}$
by a sequence of
$S^{3}$
by a sequence of
![]() $(\pm 1)$
-contact surgeries. However, we know from [Reference Eliashberg10, Reference Gompf19] that a contact manifold
$(\pm 1)$
-contact surgeries. However, we know from [Reference Eliashberg10, Reference Gompf19] that a contact manifold
![]() $(M,\xi )$
is Stein fillable if and only if there exists a directed path from
$(M,\xi )$
is Stein fillable if and only if there exists a directed path from
![]() $v_{(\#_{k} S^{1}\times S^{2},\xi _{\mathrm {st}})}$
to
$v_{(\#_{k} S^{1}\times S^{2},\xi _{\mathrm {st}})}$
to
![]() $v_{(M,\xi )}$
and thus
$v_{(M,\xi )}$
and thus
![]() $\Gamma $
is not strongly connected since there exist non-Stein fillable contact manifolds. (Recall that an oriented graph is strongly connected if for any pair of vertices
$\Gamma $
is not strongly connected since there exist non-Stein fillable contact manifolds. (Recall that an oriented graph is strongly connected if for any pair of vertices
![]() $(v_{1},v_{2})$
there exists a path from
$(v_{1},v_{2})$
there exists a path from
![]() $v_{1}$
to
$v_{1}$
to
![]() $v_{2}$
following the orientations of the edges.) Etnyre–Honda [Reference Etnyre and Honda15] showed that there exists a directed path from any vertex corresponding to a given overtwisted contact manifold to any other vertex, that is,
$v_{2}$
following the orientations of the edges.) Etnyre–Honda [Reference Etnyre and Honda15] showed that there exists a directed path from any vertex corresponding to a given overtwisted contact manifold to any other vertex, that is,
![]() $\Gamma $
is strongly connected from any vertex corresponding to an overtwisted contact manifold. The question whether there exists a vertex such that
$\Gamma $
is strongly connected from any vertex corresponding to an overtwisted contact manifold. The question whether there exists a vertex such that
![]() $\Gamma $
is strongly connected to that vertex is equivalent to the open question whether there exists a maximal element with respect to the Stein cobordism relation [Reference Wendl32].
$\Gamma $
is strongly connected to that vertex is equivalent to the open question whether there exists a maximal element with respect to the Stein cobordism relation [Reference Wendl32].
We show that
![]() $\Gamma $
stays connected after removing an arbitrary finite collection of vertices and edges. Recall that a graph is called k-connected if it is still connected after removing k arbitrary vertices and k-edge-connected if it remains connected after removing k arbitrary edges.
$\Gamma $
stays connected after removing an arbitrary finite collection of vertices and edges. Recall that a graph is called k-connected if it is still connected after removing k arbitrary vertices and k-edge-connected if it remains connected after removing k arbitrary edges.
Theorem 1.1. The contact surgery graph
![]() $\Gamma $
is k-connected and k-edge-connected for any integer
$\Gamma $
is k-connected and k-edge-connected for any integer
![]() $k\geq 0$
.
$k\geq 0$
.
We equip
![]() $\Gamma $
with its graph metric
$\Gamma $
with its graph metric
![]() $\textrm {d}$
. Then the distance from
$\textrm {d}$
. Then the distance from
![]() $v_{(S^{3},\xi _{\mathrm {st}})}$
to another vertex
$v_{(S^{3},\xi _{\mathrm {st}})}$
to another vertex
![]() $v_{(M,\xi )}$
equals the contact
$v_{(M,\xi )}$
equals the contact
![]() $(\pm 1)$
-surgery number
$(\pm 1)$
-surgery number
![]() $\operatorname {\mathrm {cs}}_{\pm 1}(M,\xi )$
, that is, the minimal number of components of a contact
$\operatorname {\mathrm {cs}}_{\pm 1}(M,\xi )$
, that is, the minimal number of components of a contact
![]() $(\pm 1)$
-surgery link L in
$(\pm 1)$
-surgery link L in
![]() $(S^{3},\xi _{\mathrm {st}})$
describing
$(S^{3},\xi _{\mathrm {st}})$
describing
![]() $(M,\xi )$
[Reference Etnyre, Kegel and Onaran16].
$(M,\xi )$
[Reference Etnyre, Kegel and Onaran16].
Proposition 1.2. The contact surgery graph
![]() $\Gamma $
has infinite diameter, infinite indegree and infinite outdegree.
$\Gamma $
has infinite diameter, infinite indegree and infinite outdegree.
Next, we study the existence of Euler and Hamiltonian walks and paths. We first recall the necessary definitions. A track t in
![]() $\Gamma $
is an infinite sequence whose terms are alternately vertices and edges of
$\Gamma $
is an infinite sequence whose terms are alternately vertices and edges of
![]() $\Gamma $
starting at a vertex and such that any edge in t joins the vertices preceding and following the edge in t. A Hamiltonian walk of
$\Gamma $
starting at a vertex and such that any edge in t joins the vertices preceding and following the edge in t. A Hamiltonian walk of
![]() $\Gamma $
is a track running through any vertex of
$\Gamma $
is a track running through any vertex of
![]() $\Gamma $
at least once. A Hamiltonian path (Eulerian path) of
$\Gamma $
at least once. A Hamiltonian path (Eulerian path) of
![]() $\Gamma $
is a track running through any vertex (edge) of
$\Gamma $
is a track running through any vertex (edge) of
![]() $\Gamma $
exactly once. If a track is following the direction of the oriented edges, it is called a ditrack and then the definitions of Hamiltonian diwalks and Hamiltonian and Eulerian dipaths are obvious.
$\Gamma $
exactly once. If a track is following the direction of the oriented edges, it is called a ditrack and then the definitions of Hamiltonian diwalks and Hamiltonian and Eulerian dipaths are obvious.
Theorem 1.3. The contact surgery graph
![]() $\Gamma $
admits Eulerian and Hamiltonian paths and also Hamiltonian walks. However, there exists no Hamiltonian diwalk, no Hamiltonian dipath and no Eulerian dipath in
$\Gamma $
admits Eulerian and Hamiltonian paths and also Hamiltonian walks. However, there exists no Hamiltonian diwalk, no Hamiltonian dipath and no Eulerian dipath in
![]() $\Gamma $
.
$\Gamma $
.
1.2 Contact geometric subgraphs of
 $\Gamma $
$\Gamma $
In Section 3, we study interesting contact geometric subgraphs of
![]() $\Gamma $
. We define the subgraphs
$\Gamma $
. We define the subgraphs
![]() $\Gamma _{\textrm {OT}}$
,
$\Gamma _{\textrm {OT}}$
,
![]() $\Gamma _{\textrm {tight}}$
,
$\Gamma _{\textrm {tight}}$
,
![]() $\Gamma _{\textrm {Stein}}$
,
$\Gamma _{\textrm {Stein}}$
,
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
consisting of vertices (and the corresponding edges connecting two such vertices) of
$\Gamma _{\textrm {c}\neq 0}$
consisting of vertices (and the corresponding edges connecting two such vertices) of
![]() $\Gamma $
representing contact manifolds which are overtwisted, tight, Stein fillable, strongly fillable, weakly fillable or with a nonvanishing contact class
$\Gamma $
representing contact manifolds which are overtwisted, tight, Stein fillable, strongly fillable, weakly fillable or with a nonvanishing contact class
![]() $\textrm {c}$
in Heegaard Floer homology. We analyse some of the basic properties of these subgraphs and in particular prove the following results.
$\textrm {c}$
in Heegaard Floer homology. We analyse some of the basic properties of these subgraphs and in particular prove the following results.
Theorem 1.4.
![]() $\Gamma _{\mathrm{OT}}$
is strongly connected. Each of
$\Gamma _{\mathrm{OT}}$
is strongly connected. Each of
![]() $\Gamma _{\mathrm{tight}}$
,
$\Gamma _{\mathrm{tight}}$
,
![]() $\Gamma _{\mathrm{Stein}}$
,
$\Gamma _{\mathrm{Stein}}$
,
![]() $\Gamma _{\mathrm{strong}}$
,
$\Gamma _{\mathrm{strong}}$
,
![]() $\Gamma _{\mathrm{weak}}$
and
$\Gamma _{\mathrm{weak}}$
and
![]() $\Gamma _{\mathrm{c}\neq 0}$
is connected, but not strongly connected.
$\Gamma _{\mathrm{c}\neq 0}$
is connected, but not strongly connected.
Theorem 1.5. There exists no Hamiltonian diwalk in each of
![]() $\Gamma _{\mathrm{tight}}$
,
$\Gamma _{\mathrm{tight}}$
,
![]() $\Gamma _{\mathrm{Stein}}$
,
$\Gamma _{\mathrm{Stein}}$
,
![]() $\Gamma _{\mathrm{strong}}$
,
$\Gamma _{\mathrm{strong}}$
,
![]() $\Gamma _{\mathrm{weak}}$
and
$\Gamma _{\mathrm{weak}}$
and
![]() $\Gamma _{\mathrm{c}\neq 0}$
, and thus also no Hamiltonian or Eulerian dipath. On the contrary,
$\Gamma _{\mathrm{c}\neq 0}$
, and thus also no Hamiltonian or Eulerian dipath. On the contrary,
![]() $\Gamma _{\mathrm{OT}}$
admits an Eulerian dipath and thus also a Hamiltonian diwalk.
$\Gamma _{\mathrm{OT}}$
admits an Eulerian dipath and thus also a Hamiltonian diwalk.
1.3 Topological subgraphs of
 $\Gamma $
$\Gamma $
In Section 4, we concentrate on topological subgraphs of the contact surgery graph. Let
![]() $\Gamma _{M}$
denote the subgraph that consists of vertices corresponding to contact manifolds where the underlying topological manifolds are all diffeomorphic to a fixed manifold M. Similarly, we denote by
$\Gamma _{M}$
denote the subgraph that consists of vertices corresponding to contact manifolds where the underlying topological manifolds are all diffeomorphic to a fixed manifold M. Similarly, we denote by
![]() $\Gamma _{(M,\mathfrak s)}$
the subgraph of
$\Gamma _{(M,\mathfrak s)}$
the subgraph of
![]() $\Gamma _{M}$
consisting of all contact structures on a fixed manifold M lying in the same
$\Gamma _{M}$
consisting of all contact structures on a fixed manifold M lying in the same
![]() $spin^{c}$
structure
$spin^{c}$
structure
![]() $\mathfrak s$
.
$\mathfrak s$
.
Theorem 1.6. The connected components of
![]() $\Gamma _{M}$
are given by
$\Gamma _{M}$
are given by
![]() $\Gamma _{(M,\mathfrak s)}$
, and thus the connected components of
$\Gamma _{(M,\mathfrak s)}$
, and thus the connected components of
![]() $\Gamma _{M}$
are in bijection with
$\Gamma _{M}$
are in bijection with
![]() $H_{1}(M)$
.
$H_{1}(M)$
.
The link
![]() $\operatorname {\mathrm {lk}}(M,\xi )$
of a contact
$\operatorname {\mathrm {lk}}(M,\xi )$
of a contact
![]() $3$
-manifold
$3$
-manifold
![]() $(M,\xi )$
is defined as
$(M,\xi )$
is defined as
In [Reference Hoffman and Walsh21], it is shown that the link of
![]() $S^{3}$
in the topological surgery graph is connected and of bounded diameter. The main question still remains open: Is the link of any topological
$S^{3}$
in the topological surgery graph is connected and of bounded diameter. The main question still remains open: Is the link of any topological
![]() $3$
-manifold connected? It turns out that we can answer this question for contact
$3$
-manifold connected? It turns out that we can answer this question for contact
![]() $3$
-manifolds.
$3$
-manifolds.
Theorem 1.7. The link
![]() $\operatorname {\mathrm {lk}}(M,\xi )$
of any contact
$\operatorname {\mathrm {lk}}(M,\xi )$
of any contact
![]() $3$
-manifold
$3$
-manifold
![]() $(M,\xi )$
is connected and of diameter less than
$(M,\xi )$
is connected and of diameter less than
![]() $4$
.
$4$
.
Conventions. Throughout this paper, we work in the smooth category. We assume all
![]() $3$
-manifolds to be connected, closed, oriented and smooth; all contact structures are positive and coorientable. For background on contact surgery and symplectic and Stein cobordisms, we refer to [Reference Casals, Etnyre and Kegel2, Reference Ding and Geiges4, Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8, Reference Etnyre, Kegel and Onaran16, Reference Geiges17, Reference Gompf and Stipsicz20, Reference Kegel22, Reference Wendl32]. Legendrian links in
$3$
-manifolds to be connected, closed, oriented and smooth; all contact structures are positive and coorientable. For background on contact surgery and symplectic and Stein cobordisms, we refer to [Reference Casals, Etnyre and Kegel2, Reference Ding and Geiges4, Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8, Reference Etnyre, Kegel and Onaran16, Reference Geiges17, Reference Gompf and Stipsicz20, Reference Kegel22, Reference Wendl32]. Legendrian links in
![]() $(S^{3},\xi _{\mathrm {st}})$
are always presented in their front projection. We choose the normalisation of the
$(S^{3},\xi _{\mathrm {st}})$
are always presented in their front projection. We choose the normalisation of the
![]() $\operatorname {\mathrm {d}}_{3}$
-invariant as in [Reference Casals, Etnyre and Kegel2, Reference Etnyre, Kegel and Onaran16] which differs from the normalisations in [Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8, Reference Gompf19] by
$\operatorname {\mathrm {d}}_{3}$
-invariant as in [Reference Casals, Etnyre and Kegel2, Reference Etnyre, Kegel and Onaran16] which differs from the normalisations in [Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8, Reference Gompf19] by
![]() $1/2$
. Using our normalisation, we see that contact structures on homology spheres have integral
$1/2$
. Using our normalisation, we see that contact structures on homology spheres have integral
![]() $\operatorname {\mathrm {d}}_{3}$
-invariants (in particular,
$\operatorname {\mathrm {d}}_{3}$
-invariants (in particular,
![]() $\operatorname {\mathrm {d}}_{3}(S^{3},\xi _{\mathrm {st}})=0$
) and that the
$\operatorname {\mathrm {d}}_{3}(S^{3},\xi _{\mathrm {st}})=0$
) and that the
![]() $\operatorname {\mathrm {d}}_{3}$
-invariant is additive under connected sums.
$\operatorname {\mathrm {d}}_{3}$
-invariant is additive under connected sums.
2 Properties of the contact surgery graph
We start by discussing the basic properties of the contact surgery graph
![]() $\Gamma $
.
$\Gamma $
.
Proof of Proposition 1.2.
![]() $\Gamma $
has infinite diameter since a single surgery can change the rank of the first homology at most by one.
$\Gamma $
has infinite diameter since a single surgery can change the rank of the first homology at most by one.
To show that the outdegree of
![]() $\Gamma $
is infinite, let
$\Gamma $
is infinite, let
![]() $v_{(M,\xi )}$
be a vertex of
$v_{(M,\xi )}$
be a vertex of
![]() $\Gamma $
. For an even integer n, choose a Legendrian knot L in a Darboux ball in
$\Gamma $
. For an even integer n, choose a Legendrian knot L in a Darboux ball in
![]() $(M,\xi )$
with Thurston–Bennequin invariant
$(M,\xi )$
with Thurston–Bennequin invariant
![]() $\operatorname {\mathrm {tb}}=1$
and rotation number
$\operatorname {\mathrm {tb}}=1$
and rotation number
![]() $\operatorname {\mathrm {rot}}=n$
. Denote the contact manifold obtained by contact
$\operatorname {\mathrm {rot}}=n$
. Denote the contact manifold obtained by contact
![]() $(-1)$
-surgery along L by
$(-1)$
-surgery along L by
![]() $L(-1)$
. A calculation, as for example in [Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8], shows that the homology of
$L(-1)$
. A calculation, as for example in [Reference Ding, Geiges and Stipsicz6, Reference Durst and Kegel8], shows that the homology of
![]() $L(-1)$
is
$L(-1)$
is
where the
![]() $\mathbb {Z}$
-summand is generated by a meridian
$\mathbb {Z}$
-summand is generated by a meridian
![]() $\mu _{L}$
of L, and that the Poincaré dual of the Euler class
$\mu _{L}$
of L, and that the Poincaré dual of the Euler class
![]() $\operatorname {\mathrm {e}}(L(-1))$
is given by
$\operatorname {\mathrm {e}}(L(-1))$
is given by
where
![]() $\operatorname {\mathrm {e}}(M,\xi )$
denotes the Poincaré dual of the Euler class of
$\operatorname {\mathrm {e}}(M,\xi )$
denotes the Poincaré dual of the Euler class of
![]() $(M,\xi )$
. Thus, we get infinitely many different contact manifolds by contact
$(M,\xi )$
. Thus, we get infinitely many different contact manifolds by contact
![]() $(-1)$
-surgery from M. The same construction with contact
$(-1)$
-surgery from M. The same construction with contact
![]() $(+1)$
-surgery along a Legendrian knot with Thurston–Bennequin invariant
$(+1)$
-surgery along a Legendrian knot with Thurston–Bennequin invariant
![]() $\operatorname {\mathrm {tb}} = -1$
provides the fact that the indegree is also infinite.
$\operatorname {\mathrm {tb}} = -1$
provides the fact that the indegree is also infinite.
Proof of Theorem 1.1.
Let E be a set consisting of k-different vertices in
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $(M_{0},\xi _{0})$
and
$(M_{0},\xi _{0})$
and
![]() $(M_{n},\xi _{n})$
be two contact
$(M_{n},\xi _{n})$
be two contact
![]() $3$
-manifolds representing vertices in
$3$
-manifolds representing vertices in
![]() $\Gamma \!\setminus \!E$
. We consider a path
$\Gamma \!\setminus \!E$
. We consider a path
in
![]() $\Gamma $
between
$\Gamma $
between
![]() $(M_{0},\xi _{0})$
and
$(M_{0},\xi _{0})$
and
![]() $(M_{n},\xi _{n})$
. We denote by
$(M_{n},\xi _{n})$
. We denote by
![]() $L_{0}$
a Legendrian surgery link in
$L_{0}$
a Legendrian surgery link in
![]() $(S^{3},\xi _{\mathrm {st}})$
representing
$(S^{3},\xi _{\mathrm {st}})$
representing
![]() $(M_{0},\xi _{0})$
. Let
$(M_{0},\xi _{0})$
. Let
![]() $K_{i+1}$
be a Legendrian knot in
$K_{i+1}$
be a Legendrian knot in
![]() $(M_{i},\xi _{i})$
such that contact
$(M_{i},\xi _{i})$
such that contact
![]() $(\pm 1)$
-surgery along
$(\pm 1)$
-surgery along
![]() $K_{i}$
is contactomorphic to
$K_{i}$
is contactomorphic to
![]() $(M_{i+1},\xi _{i+1})$
. By Lemma 4.7.1 in [Reference Kegel22], we can represent
$(M_{i+1},\xi _{i+1})$
. By Lemma 4.7.1 in [Reference Kegel22], we can represent
![]() $K_{1}$
as a Legendrian knot in the complement of
$K_{1}$
as a Legendrian knot in the complement of
![]() $L_{0}$
and thus
$L_{0}$
and thus
![]() $L_{1}:=L\cup K_{1}$
is a surgery link in
$L_{1}:=L\cup K_{1}$
is a surgery link in
![]() $(S^{3},\xi _{\mathrm {st}})$
for
$(S^{3},\xi _{\mathrm {st}})$
for
![]() $(M_{1},\xi _{1})$
. By induction, we get surgery links
$(M_{1},\xi _{1})$
. By induction, we get surgery links
![]() $L_{i}$
in
$L_{i}$
in
![]() $(S^{3},\xi _{\mathrm {st}})$
representing
$(S^{3},\xi _{\mathrm {st}})$
representing
![]() $(M_{i},\xi _{i})$
describing the above path in
$(M_{i},\xi _{i})$
describing the above path in
![]() $\Gamma $
. We will construct a path from
$\Gamma $
. We will construct a path from
![]() $(M_{0},\xi _{0})$
to
$(M_{0},\xi _{0})$
to
![]() $(M_{n},\xi _{n})$
in
$(M_{n},\xi _{n})$
in
![]() $\Gamma \!\setminus \!E$
.
$\Gamma \!\setminus \!E$
.
Let
![]() $p\geq 2$
be an integer such that no contact structure on
$p\geq 2$
be an integer such that no contact structure on
![]() $M_{i}\#L(p,1)$
is in E for all
$M_{i}\#L(p,1)$
is in E for all
![]() $i=0,\ldots ,n$
. (Such a p exists because E is finite.) We define a new sequence of Legendrian surgery links as follows. We set
$i=0,\ldots ,n$
. (Such a p exists because E is finite.) We define a new sequence of Legendrian surgery links as follows. We set
![]() $L^{\prime }_{0}=L_{0}$
and
$L^{\prime }_{0}=L_{0}$
and
![]() $L^{\prime }_{i+1}=L_{i}\sqcup U_{p}(-1)$
, where
$L^{\prime }_{i+1}=L_{i}\sqcup U_{p}(-1)$
, where
![]() $\sqcup $
denotes the disjoint union of knots and
$\sqcup $
denotes the disjoint union of knots and
![]() $U_{p}(-1)$
denotes the contact
$U_{p}(-1)$
denotes the contact
![]() $(-1)$
-surgery along a Legendrian unknot with
$(-1)$
-surgery along a Legendrian unknot with
![]() $\operatorname {\mathrm {tb}}=1-p$
. It follows that
$\operatorname {\mathrm {tb}}=1-p$
. It follows that
![]() $L^{\prime }_{i+1}$
represents a contact structure on
$L^{\prime }_{i+1}$
represents a contact structure on
![]() $M_{i}\#L(p,1)$
. Finally, we set
$M_{i}\#L(p,1)$
. Finally, we set
![]() $L^{\prime }_{n+2}$
to be the disjoint union of
$L^{\prime }_{n+2}$
to be the disjoint union of
![]() $L_{n}$
with
$L_{n}$
with
![]() $U_{p}(-1)$
together with a
$U_{p}(-1)$
together with a
![]() $(+1)$
-framed meridian
$(+1)$
-framed meridian
![]() $\mu _{U_{p}}$
of
$\mu _{U_{p}}$
of
![]() $U_{p}$
. Since
$U_{p}$
. Since
![]() $U_{p}(-1)\cup \mu _{U_{p}}(+1)$
yields
$U_{p}(-1)\cup \mu _{U_{p}}(+1)$
yields
![]() $(S^{3},\xi _{\mathrm {st}})$
by [Reference Avdek1], we see that
$(S^{3},\xi _{\mathrm {st}})$
by [Reference Avdek1], we see that
![]() $L^{\prime }_{n+2}$
represents
$L^{\prime }_{n+2}$
represents
![]() $(M_{n},\xi _{n})$
. Thus, a path in
$(M_{n},\xi _{n})$
. Thus, a path in
![]() $\Gamma \!\setminus \!E$
between
$\Gamma \!\setminus \!E$
between
![]() $(M_{0},\xi _{0})$
and
$(M_{0},\xi _{0})$
and
![]() $(M_{n},\xi _{n})$
is constructed. The same argument shows that
$(M_{n},\xi _{n})$
is constructed. The same argument shows that
![]() $\Gamma $
is also k-edge connected.
$\Gamma $
is also k-edge connected.
In fact, the above proof directly implies the following corollary.
Corollary 2.1. Let E be a finite set of vertices in
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $(M_{1},\xi _{1})$
and
$(M_{1},\xi _{1})$
and
![]() $(M_{2},\xi _{2})$
be two vertices in
$(M_{2},\xi _{2})$
be two vertices in
![]() $\Gamma \!\setminus \!E$
. Then their distances in the corresponding graphs are related by
$\Gamma \!\setminus \!E$
. Then their distances in the corresponding graphs are related by
With the above results, we study the existence of Eulerian and Hamiltonian paths and walks.
Proof of Theorem 1.3.
Since
![]() $\Gamma $
is connected, k-connected and k-edge-connected, for any natural number k, and of infinite degree, the main results from [Reference Erdős, Grünwald and Vázsonyi13, Reference Erdős, Grünwald and Vázsonyi14, Reference Nash-Williams26] immediately imply that
$\Gamma $
is connected, k-connected and k-edge-connected, for any natural number k, and of infinite degree, the main results from [Reference Erdős, Grünwald and Vázsonyi13, Reference Erdős, Grünwald and Vázsonyi14, Reference Nash-Williams26] immediately imply that
![]() $\Gamma $
contains Eulerian and Hamiltonian paths.
$\Gamma $
contains Eulerian and Hamiltonian paths.
Since contact
![]() $(-1)$
-surgery preserves tightness by [Reference Wand29], a Hamiltonian diwalk has to start at an overtwisted contact manifold and has to run first through all overtwisted contact manifolds before reaching a tight contact manifold. However, since there exists infinitely many overtwisted contact manifolds, this is not possible.
$(-1)$
-surgery preserves tightness by [Reference Wand29], a Hamiltonian diwalk has to start at an overtwisted contact manifold and has to run first through all overtwisted contact manifolds before reaching a tight contact manifold. However, since there exists infinitely many overtwisted contact manifolds, this is not possible.
Using the main result of [Reference Nash-Williams25], we deduce the following corollary.
Corollary 2.2.
![]() $\Gamma $
is biased, that is, there exists a subset X of the vertices of
$\Gamma $
is biased, that is, there exists a subset X of the vertices of
![]() $\Gamma $
such that there are infinitely many edges oriented from X to its complement
$\Gamma $
such that there are infinitely many edges oriented from X to its complement
![]() $X^{c}$
, but only finitely many edges oriented from
$X^{c}$
, but only finitely many edges oriented from
![]() $X^{c}$
to X.
$X^{c}$
to X.
It would be interesting to find such a set X explicitly.
Proof of Corollary 2.2.
The main result of [Reference Nash-Williams25] says that an oriented graph admits an Eulerian dipath based at a vertex v if and only if the graph is countable, connected,
![]() $1$
-coherent, v-solenoidal and unbiased. We refer to [Reference Nash-Williams25] for the definitions. Since the contact surgery graph
$1$
-coherent, v-solenoidal and unbiased. We refer to [Reference Nash-Williams25] for the definitions. Since the contact surgery graph
![]() $\Gamma $
is connected and countable but admits no Eulerian dipath, it is enough to check that
$\Gamma $
is connected and countable but admits no Eulerian dipath, it is enough to check that
![]() $\Gamma $
is
$\Gamma $
is
![]() $1$
-coherent and v-solenoidal. First,
$1$
-coherent and v-solenoidal. First,
![]() $1$
-coherency is a condition of the underlying unoriented graph and since
$1$
-coherency is a condition of the underlying unoriented graph and since
![]() $\Gamma $
admits an undirected Euler path,
$\Gamma $
admits an undirected Euler path,
![]() $\Gamma $
is
$\Gamma $
is
![]() $1$
-coherent. Second, it follows that
$1$
-coherent. Second, it follows that
![]() $\Gamma $
is v-solenoidal for any vertex since the indegree and outdegree are infinite for any vertex.
$\Gamma $
is v-solenoidal for any vertex since the indegree and outdegree are infinite for any vertex.
3 Contact geometric subgraphs of
 $\Gamma $
$\Gamma $
Here we study the subgraphs
![]() $\Gamma _{\textrm {OT}}$
,
$\Gamma _{\textrm {OT}}$
,
![]() $\Gamma _{\textrm {tight}}$
,
$\Gamma _{\textrm {tight}}$
,
![]() $\Gamma _{\textrm {Stein}}$
,
$\Gamma _{\textrm {Stein}}$
,
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
.
$\Gamma _{\textrm {c}\neq 0}$
.
Proof of Theorem 1.4.
We first show that
![]() $\Gamma _{\textrm {OT}}$
is strongly connected. Let
$\Gamma _{\textrm {OT}}$
is strongly connected. Let
![]() $(M_{1},\xi _{1})$
and
$(M_{1},\xi _{1})$
and
![]() $(M_{2},\xi _{2})$
be two overtwisted contact manifolds. By [Reference Etnyre and Honda15], there exist a directed path p from
$(M_{2},\xi _{2})$
be two overtwisted contact manifolds. By [Reference Etnyre and Honda15], there exist a directed path p from
![]() $(M_{1},\xi _{1})$
to
$(M_{1},\xi _{1})$
to
![]() $(M_{2},\xi _{2})$
in
$(M_{2},\xi _{2})$
in
![]() $\Gamma $
. We argue that any vertex in p corresponds to an overtwisted contact manifold. Let us assume the contrary. Since
$\Gamma $
. We argue that any vertex in p corresponds to an overtwisted contact manifold. Let us assume the contrary. Since
![]() $(M_{2},\xi _{2})$
is overtwisted, there exists an overtwisted contact manifold
$(M_{2},\xi _{2})$
is overtwisted, there exists an overtwisted contact manifold
![]() $(M_{\textrm {OT}},\xi _{\textrm {OT}})$
that can be obtained by contact
$(M_{\textrm {OT}},\xi _{\textrm {OT}})$
that can be obtained by contact
![]() $(-1)$
-surgery from a tight contact manifold
$(-1)$
-surgery from a tight contact manifold
![]() $(M_{\textrm {tight}},\xi _{\textrm {tight}})$
contradicting Wand’s result which says that contact
$(M_{\textrm {tight}},\xi _{\textrm {tight}})$
contradicting Wand’s result which says that contact
![]() $(-1)$
-surgery preserves tightness [Reference Wand29].
$(-1)$
-surgery preserves tightness [Reference Wand29].
Next, we consider
![]() $\Gamma _{*}$
with
$\Gamma _{*}$
with
![]() $*=\textrm {tight}$
,
$*=\textrm {tight}$
,
![]() $\textrm {Stein}$
,
$\textrm {Stein}$
,
![]() $\textrm {strong}$
,
$\textrm {strong}$
,
![]() $\textrm {weak}$
or
$\textrm {weak}$
or
![]() $\textrm {c}\neq 0$
. To show that
$\textrm {c}\neq 0$
. To show that
![]() $\Gamma _{*}$
is connected, we show that there exists an undirected path in
$\Gamma _{*}$
is connected, we show that there exists an undirected path in
![]() $\Gamma _{*}$
from
$\Gamma _{*}$
from
![]() $(S^{3},\xi _{\mathrm {st}})$
to any other contact manifold
$(S^{3},\xi _{\mathrm {st}})$
to any other contact manifold
![]() $(M,\xi )$
with property
$(M,\xi )$
with property
![]() $*$
. We consider the contact
$*$
. We consider the contact
![]() $(+1)$
-surgery along the Legendrian unknot with Thurston–Bennequin invariant
$(+1)$
-surgery along the Legendrian unknot with Thurston–Bennequin invariant
![]() $\operatorname {\mathrm {tb}}=-2$
and rotation number
$\operatorname {\mathrm {tb}}=-2$
and rotation number
![]() $\operatorname {\mathrm {rot}}=1$
in
$\operatorname {\mathrm {rot}}=1$
in
![]() $(S^{3},\xi _{\mathrm {st}})$
. It is well known that the resulting contact manifold is the overtwisted contact structure
$(S^{3},\xi _{\mathrm {st}})$
. It is well known that the resulting contact manifold is the overtwisted contact structure
![]() $\xi _{1}$
on
$\xi _{1}$
on
![]() $S^{3}$
with normalised
$S^{3}$
with normalised
![]() $\mathrm{d}_{3}$
-invariant equal to
$\mathrm{d}_{3}$
-invariant equal to
![]() $1$
[Reference Ding, Geiges and Stipsicz6]. Then by [Reference Etnyre and Honda15], there exists a directed path in
$1$
[Reference Ding, Geiges and Stipsicz6]. Then by [Reference Etnyre and Honda15], there exists a directed path in
![]() $\Gamma $
of contact
$\Gamma $
of contact
![]() $(-1)$
-surgeries from
$(-1)$
-surgeries from
![]() $(S^{3},\xi _{1})$
to
$(S^{3},\xi _{1})$
to
![]() $(M,\xi )$
. However, this path runs through at least one overtwisted contact manifold and hence it is not in
$(M,\xi )$
. However, this path runs through at least one overtwisted contact manifold and hence it is not in
![]() $\Gamma _{*}$
. In total, we get a surgery link L in
$\Gamma _{*}$
. In total, we get a surgery link L in
![]() $(S^{3},\xi _{\mathrm {st}})$
describing
$(S^{3},\xi _{\mathrm {st}})$
describing
![]() $(M,\xi )$
with only a single contact surgery coefficient
$(M,\xi )$
with only a single contact surgery coefficient
![]() $(+1)$
. Now we change the order of the surgeries and first perform all contact
$(+1)$
. Now we change the order of the surgeries and first perform all contact
![]() $(-1)$
-surgeries and at the end, we perform the single contact
$(-1)$
-surgeries and at the end, we perform the single contact
![]() $(+1)$
-surgery. Since contact
$(+1)$
-surgery. Since contact
![]() $(-1)$
-surgery is known to preserve any of the properties
$(-1)$
-surgery is known to preserve any of the properties
![]() $*$
by [Reference Eliashberg10, Reference Ozsváth and Szabó27, Reference Wand29, Reference Weinstein30], we get a path in
$*$
by [Reference Eliashberg10, Reference Ozsváth and Szabó27, Reference Wand29, Reference Weinstein30], we get a path in
![]() $\Gamma _{*}$
from
$\Gamma _{*}$
from
![]() $(S^{3},\xi _{\mathrm {st}})$
to
$(S^{3},\xi _{\mathrm {st}})$
to
![]() $(M,\xi )$
.
$(M,\xi )$
.
The contact surgery subgraphs
![]() $\Gamma _{\textrm {tight}}$
,
$\Gamma _{\textrm {tight}}$
,
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
are not strongly connected since there exists in each of these graphs a contact manifold
$\Gamma _{\textrm {c}\neq 0}$
are not strongly connected since there exists in each of these graphs a contact manifold
![]() $(M,\xi )$
which is not Stein fillable [Reference Eliashberg12, Reference Ghiggini18] and then there cannot be a directed path from
$(M,\xi )$
which is not Stein fillable [Reference Eliashberg12, Reference Ghiggini18] and then there cannot be a directed path from
![]() $(S^{3},\xi _{\mathrm {st}})$
to
$(S^{3},\xi _{\mathrm {st}})$
to
![]() $(M,\xi )$
.
$(M,\xi )$
.
Finally, we show that
![]() $\Gamma _{\textrm {Stein}}$
is not strongly connected. We show that there exists no directed path of contact
$\Gamma _{\textrm {Stein}}$
is not strongly connected. We show that there exists no directed path of contact
![]() $(-1)$
-surgeries from
$(-1)$
-surgeries from
![]() $(S^{3},\xi _{\mathrm {st}})$
to
$(S^{3},\xi _{\mathrm {st}})$
to
![]() $(S^{1}\times S^{2},\xi _{\mathrm {st}})$
. Let us assume the contrary. Then there must be a simply connected Stein cobordism from
$(S^{1}\times S^{2},\xi _{\mathrm {st}})$
. Let us assume the contrary. Then there must be a simply connected Stein cobordism from
![]() $(S^{3},\xi _{\mathrm {st}})$
to
$(S^{3},\xi _{\mathrm {st}})$
to
![]() ${(S^{1}\times S^{2},\xi _{\mathrm {st}})}$
. We glue this Stein cobordism to the standard
${(S^{1}\times S^{2},\xi _{\mathrm {st}})}$
. We glue this Stein cobordism to the standard
![]() $4$
-ball filling of
$4$
-ball filling of
![]() $(S^{3},\xi _{\mathrm {st}})$
to get a simply connected Stein filling
$(S^{3},\xi _{\mathrm {st}})$
to get a simply connected Stein filling
![]() $(W,\omega _{\mathrm {st}})$
of
$(W,\omega _{\mathrm {st}})$
of
![]() $(S^{1}\times S^{2},\xi _{\mathrm {st}})$
. However, by [Reference Eliashberg10], any Stein filling of
$(S^{1}\times S^{2},\xi _{\mathrm {st}})$
. However, by [Reference Eliashberg10], any Stein filling of
![]() $(S^{1}\times S^{2},\xi _{\mathrm {st}})$
is diffeomorphic to
$(S^{1}\times S^{2},\xi _{\mathrm {st}})$
is diffeomorphic to
![]() $S^{1}\times D^{3}$
which is not simply connected.
$S^{1}\times D^{3}$
which is not simply connected.
Remark 3.1. We remark that we have shown that
![]() $\Gamma _{\mathrm{OT}}$
is a strongly connected component of
$\Gamma _{\mathrm{OT}}$
is a strongly connected component of
![]() $\Gamma $
and we wonder what are the other strongly connected components of
$\Gamma $
and we wonder what are the other strongly connected components of
![]() $\Gamma $
. Using Wendl’s theorem on symplectic fillings of planar contact manifolds [Reference Wendl31], Plamenevskaya [Reference Plamenevskaya28] deduced that any planar Stein fillable contact manifold
$\Gamma $
. Using Wendl’s theorem on symplectic fillings of planar contact manifolds [Reference Wendl31], Plamenevskaya [Reference Plamenevskaya28] deduced that any planar Stein fillable contact manifold
![]() $(M,\xi )$
cannot be obtained from itself by a sequence of contact
$(M,\xi )$
cannot be obtained from itself by a sequence of contact
![]() $(-1)$
-surgeries. It follows that any planar Stein fillable contact manifold is its own strongly connected component.
$(-1)$
-surgeries. It follows that any planar Stein fillable contact manifold is its own strongly connected component.
Question 3.2. Is
![]() $\Gamma _{\mathrm{OT}}$
the only nontrivial strongly connected component of
$\Gamma _{\mathrm{OT}}$
the only nontrivial strongly connected component of
![]() $\Gamma $
?
$\Gamma $
?
Remark 3.3. We know that each of
![]() $\Gamma _{\textrm {OT}}$
,
$\Gamma _{\textrm {OT}}$
,
![]() $\Gamma _{\textrm {tight}}$
,
$\Gamma _{\textrm {tight}}$
,
![]() $\Gamma _{\textrm {Stein}}$
,
$\Gamma _{\textrm {Stein}}$
,
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
has infinite diameter and infinite in- and outdegree. That
$\Gamma _{\textrm {c}\neq 0}$
has infinite diameter and infinite in- and outdegree. That
![]() $\Gamma _{\textrm {tight}}$
and
$\Gamma _{\textrm {tight}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
have infinite indegree follows from the work of Lisca–Stipsicz [Reference Lisca and Stipsicz23]. As part of their main theorem, they describe infinitely many different Legendrian knots such that contact
$\Gamma _{\textrm {c}\neq 0}$
have infinite indegree follows from the work of Lisca–Stipsicz [Reference Lisca and Stipsicz23]. As part of their main theorem, they describe infinitely many different Legendrian knots such that contact
![]() $(+1)$
-surgery on them yields tight contact manifolds with nonvanishing contact class. That
$(+1)$
-surgery on them yields tight contact manifolds with nonvanishing contact class. That
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {Stein}}$
have infinite indegree follows similarly from [Reference Conway, Etnyre and Tosun3]. The other statements follow from the arguments in the proof of Proposition 1.2.
$\Gamma _{\textrm {Stein}}$
have infinite indegree follows similarly from [Reference Conway, Etnyre and Tosun3]. The other statements follow from the arguments in the proof of Proposition 1.2.
For the proof of Theorem 1.5, we need the following lemma.
Lemma 3.4. Let
![]() $(M,\xi ^{M})$
be an overtwisted manifold and
$(M,\xi ^{M})$
be an overtwisted manifold and
![]() $(M,\xi ^{M}_{\mathrm{stab}})$
be its stabilisation, that is,
$(M,\xi ^{M}_{\mathrm{stab}})$
be its stabilisation, that is,
![]() $(M,\xi ^{M}_{\mathrm{stab}})=(M,\xi ^{M})\#(S^{3},\xi _{1})$
. Let
$(M,\xi ^{M}_{\mathrm{stab}})=(M,\xi ^{M})\#(S^{3},\xi _{1})$
. Let
![]() $(N,\xi ^{N})$
be an overtwisted contact manifold which can be obtained from
$(N,\xi ^{N})$
be an overtwisted contact manifold which can be obtained from
![]() $(M,\xi ^{M}_{\mathrm{stab}})$
by a single contact
$(M,\xi ^{M}_{\mathrm{stab}})$
by a single contact
![]() $(-1)$
-surgery. Then we can obtain
$(-1)$
-surgery. Then we can obtain
![]() $(M,\xi ^{M})$
by a contact
$(M,\xi ^{M})$
by a contact
![]() $(-1)$
-surgery from
$(-1)$
-surgery from
![]() $(N,\xi ^{N})$
.
$(N,\xi ^{N})$
.
Proof of Lemma 3.4.
Let L be a Legendrian knot in
![]() $(M,\xi ^{M}_{\textrm {stab}})$
such that
$(M,\xi ^{M}_{\textrm {stab}})$
such that
![]() $L(-1)=(N,\xi ^{N})$
. Let
$L(-1)=(N,\xi ^{N})$
. Let
![]() $L^{*}$
be the dual surgery knot of L in
$L^{*}$
be the dual surgery knot of L in
![]() $(N,\xi ^{N})$
. By the cancellation lemma,
$(N,\xi ^{N})$
. By the cancellation lemma,
![]() $L^{*}(+1)$
is again contactomorphic to
$L^{*}(+1)$
is again contactomorphic to
![]() $(M,\xi ^{M}_{\textrm {stab}})$
. Now we choose a loose Legendrian realisation
$(M,\xi ^{M}_{\textrm {stab}})$
. Now we choose a loose Legendrian realisation
![]() $L^{\prime }$
of
$L^{\prime }$
of
![]() $L^{*}$
such that if we stabilise
$L^{*}$
such that if we stabilise
![]() $L^{\prime }$
, once positive and once negative, we get a Legendrian knot which is formally isotopic to
$L^{\prime }$
, once positive and once negative, we get a Legendrian knot which is formally isotopic to
![]() $L^{*}$
. (This is possible since we can destabilise any loose Legendrian knot.)
$L^{*}$
. (This is possible since we can destabilise any loose Legendrian knot.)
We claim that
![]() $L^{\prime }(-1)$
yields
$L^{\prime }(-1)$
yields
![]() $(M,\xi ^{M})$
. Since
$(M,\xi ^{M})$
. Since
![]() $L^{\prime }$
is topologically isotopic to
$L^{\prime }$
is topologically isotopic to
![]() $L^{*}$
and its contact framing and the contact framing of
$L^{*}$
and its contact framing and the contact framing of
![]() $L^{*}$
differ by 2, the contact
$L^{*}$
differ by 2, the contact
![]() $(-1)$
-surgery along
$(-1)$
-surgery along
![]() $L^{\prime }$
yields topologically the same manifold as the contact
$L^{\prime }$
yields topologically the same manifold as the contact
![]() $(+1)$
-surgery along
$(+1)$
-surgery along
![]() $L^{*}$
, which is in fact M. Note that
$L^{*}$
, which is in fact M. Note that
![]() $L^{\prime }(-1)$
is overtwisted since
$L^{\prime }(-1)$
is overtwisted since
![]() $L^{\prime }$
is a loose knot. Then a straightforward computation in a local model, as in [Reference Ding, Geiges and Stipsicz7], shows that the homotopical invariants of the contact structures agree. Thus by Eliashberg’s classification of contact structures [Reference Eliashberg9], it follows that the contact structures are contactomorphic.
$L^{\prime }$
is a loose knot. Then a straightforward computation in a local model, as in [Reference Ding, Geiges and Stipsicz7], shows that the homotopical invariants of the contact structures agree. Thus by Eliashberg’s classification of contact structures [Reference Eliashberg9], it follows that the contact structures are contactomorphic.
Proof of Theorem 1.5.
First we remark that by following the proof of Theorem 1.1, we conclude that each of the subgraphs
![]() $\Gamma _{\textrm {OT}}$
,
$\Gamma _{\textrm {OT}}$
,
![]() $\Gamma _{\textrm {tight}}$
,
$\Gamma _{\textrm {tight}}$
,
![]() $\Gamma _{\textrm {Stein}}$
,
$\Gamma _{\textrm {Stein}}$
,
![]() $\Gamma _{\textrm {strong}}$
,
$\Gamma _{\textrm {strong}}$
,
![]() $\Gamma _{\textrm {weak}}$
and
$\Gamma _{\textrm {weak}}$
and
![]() $\Gamma _{\textrm {c}\neq 0}$
is k-connected and k-edge-connected for any natural number k. Thus, each of these subgraphs admits Eulerian and Hamiltonian paths and also Hamiltonian walks. For the directed paths, we conclude as in the proof of Theorem 1.3 that
$\Gamma _{\textrm {c}\neq 0}$
is k-connected and k-edge-connected for any natural number k. Thus, each of these subgraphs admits Eulerian and Hamiltonian paths and also Hamiltonian walks. For the directed paths, we conclude as in the proof of Theorem 1.3 that
![]() $\Gamma _{*}$
does not admit a Hamiltonian diwalk, a Hamiltonian dipath and a Eulerian dipath for
$\Gamma _{*}$
does not admit a Hamiltonian diwalk, a Hamiltonian dipath and a Eulerian dipath for
![]() $*=\textrm {tight}$
,
$*=\textrm {tight}$
,
![]() $\textrm {Stein}$
,
$\textrm {Stein}$
,
![]() $\textrm {strong}$
,
$\textrm {strong}$
,
![]() $\textrm {weak}$
or
$\textrm {weak}$
or
![]() $\textrm {c}\neq 0$
.
$\textrm {c}\neq 0$
.
However, we show that an Eulerian dipath exists in
![]() $\Gamma _{\textrm {OT}}$
. As in the proof of Corollary 2.2, it follows that
$\Gamma _{\textrm {OT}}$
. As in the proof of Corollary 2.2, it follows that
![]() $\Gamma _{\textrm {OT}}$
is
$\Gamma _{\textrm {OT}}$
is
![]() $1$
-coherent and v-solenoidal. By the main result of [Reference Nash-Williams25], it is therefore enough to show that
$1$
-coherent and v-solenoidal. By the main result of [Reference Nash-Williams25], it is therefore enough to show that
![]() $\Gamma _{\textrm {OT}}$
is unbiased. Assume there exists a subset X of the vertices of
$\Gamma _{\textrm {OT}}$
is unbiased. Assume there exists a subset X of the vertices of
![]() $\Gamma _{\textrm {OT}}$
such that there are infinitely many edges oriented from X to its complement
$\Gamma _{\textrm {OT}}$
such that there are infinitely many edges oriented from X to its complement
![]() $X^{c}$
, but only finitely many edges oriented from
$X^{c}$
, but only finitely many edges oriented from
![]() $X^{c}$
to X. As a first step, we show that there exists, for any
$X^{c}$
to X. As a first step, we show that there exists, for any
![]() $i\in \mathbb {N}$
, a Legendrian knot
$i\in \mathbb {N}$
, a Legendrian knot
![]() $K_{i}$
in an overtwisted contact manifolds
$K_{i}$
in an overtwisted contact manifolds
![]() $(M_{i},\xi _{i})$
in X such that all
$(M_{i},\xi _{i})$
in X such that all
![]() $M_{i}$
are pairwise nondiffeomorphic and the contact
$M_{i}$
are pairwise nondiffeomorphic and the contact
![]() $(-1)$
-surgery
$(-1)$
-surgery
![]() $K_{i}(-1)$
along
$K_{i}(-1)$
along
![]() $K_{i}$
lies in
$K_{i}$
lies in
![]() $X^{c}$
. (This step will not use the overtwistedness.)
$X^{c}$
. (This step will not use the overtwistedness.)
By assumption, we know that there are infinitely many edges pointing out of X. For any
![]() $i\in \mathbb {N}$
, we choose some Legendrian knot
$i\in \mathbb {N}$
, we choose some Legendrian knot
![]() $K^{\prime }_{i}$
in an overtwisted contact manifold
$K^{\prime }_{i}$
in an overtwisted contact manifold
![]() $(M,\xi )$
in X such that
$(M,\xi )$
in X such that
![]() $K^{\prime }_{i}(-1)$
lies in
$K^{\prime }_{i}(-1)$
lies in
![]() $X^{c}$
. We show that we can obtain infinitely many of the
$X^{c}$
. We show that we can obtain infinitely many of the
![]() $K^{\prime }_{i}(-1)$
by a contact
$K^{\prime }_{i}(-1)$
by a contact
![]() $(-1)$
-surgery from infinitely many different manifolds in X. For that, we first observe that we can get an overtwisted contact structure
$(-1)$
-surgery from infinitely many different manifolds in X. For that, we first observe that we can get an overtwisted contact structure
![]() $\xi _{\textrm {OT}}$
on
$\xi _{\textrm {OT}}$
on
![]() $M\# L(i+1,1)$
by a single contact
$M\# L(i+1,1)$
by a single contact
![]() $(+1)$
-surgery along a Legendrian unknot
$(+1)$
-surgery along a Legendrian unknot
![]() $U_{i}$
in a Darboux ball in
$U_{i}$
in a Darboux ball in
![]() $M\!\setminus \!K_{i}$
. Since only finitely many edges point into X, we conclude that an infinite subset of the
$M\!\setminus \!K_{i}$
. Since only finitely many edges point into X, we conclude that an infinite subset of the
![]() $(M\# L(i+1,1),\xi _{\textrm {OT}})$
are elements of X again. Performing a contact
$(M\# L(i+1,1),\xi _{\textrm {OT}})$
are elements of X again. Performing a contact
![]() $(-1)$
-surgery along
$(-1)$
-surgery along
![]() $K_{i}$
in
$K_{i}$
in
![]() $(M\# L(i+1,1),\xi _{\textrm {OT}})$
yields
$(M\# L(i+1,1),\xi _{\textrm {OT}})$
yields
![]() $K_{i}(-1)\#L(i+1,1)$
with an overtwisted contact structure. Then cancelling the contact
$K_{i}(-1)\#L(i+1,1)$
with an overtwisted contact structure. Then cancelling the contact
![]() $(+1)$
-surgery along
$(+1)$
-surgery along
![]() $U_{i}$
by a contact
$U_{i}$
by a contact
![]() $(-1)$
-surgery along a push-off of
$(-1)$
-surgery along a push-off of
![]() $U_{i}$
yields
$U_{i}$
yields
![]() $K_{i}(-1)$
. Thus we can conclude that there exists an infinite family of Legendrian knots
$K_{i}(-1)$
. Thus we can conclude that there exists an infinite family of Legendrian knots
![]() $K_{i}$
in different overtwisted contact manifolds
$K_{i}$
in different overtwisted contact manifolds
![]() $(M_{i},\xi _{i})$
in X such that
$(M_{i},\xi _{i})$
in X such that
![]() $K_{i}(-1)$
are elements of
$K_{i}(-1)$
are elements of
![]() $X^{c}$
.
$X^{c}$
.
In the next step, which only works for overtwisted contact manifolds, we show that we can get back from the
![]() $K_{i}(-1)$
to X by contact
$K_{i}(-1)$
to X by contact
![]() $(-1)$
-surgeries. We write
$(-1)$
-surgeries. We write
![]() $(M_{i},\xi _{i})$
as
$(M_{i},\xi _{i})$
as
![]() $(M,\xi _{i}^{\prime })\#(S^{3},\xi _{1})$
. By Lemma 3.4, there exists a contact
$(M,\xi _{i}^{\prime })\#(S^{3},\xi _{1})$
. By Lemma 3.4, there exists a contact
![]() $(-1)$
-surgery along a Legendrian knot in
$(-1)$
-surgery along a Legendrian knot in
![]() $K_{i}(-1)$
yielding
$K_{i}(-1)$
yielding
![]() $(M_{i},\xi _{i}^{\prime })$
, and from
$(M_{i},\xi _{i}^{\prime })$
, and from
![]() $(M_{i},\xi _{i}^{\prime })$
, we can get back to
$(M_{i},\xi _{i}^{\prime })$
, we can get back to
![]() $(M_{i},\xi _{i})$
by another contact
$(M_{i},\xi _{i})$
by another contact
![]() $(-1)$
-surgery. Thus we have constructed an infinite family of edges pointing from
$(-1)$
-surgery. Thus we have constructed an infinite family of edges pointing from
![]() $X^{c}$
into X contradicting the assumption and finishing the proof of Theorem 1.5.
$X^{c}$
into X contradicting the assumption and finishing the proof of Theorem 1.5.
Next, we study the difference of the distance functions.
Theorem 3.5. Given two overtwisted contact manifolds
![]() $(M_{1},\xi _{1})$
and
$(M_{1},\xi _{1})$
and
![]() $(M_{2},\xi _{2})$
:
$(M_{2},\xi _{2})$
:
-
(1) the distance between
 $(M_{1},\xi _{1})$
and
$(M_{1},\xi _{1})$
and
 $(M_{2},\xi _{2})$
in
$(M_{2},\xi _{2})$
in
 $\Gamma _{\mathrm{OT}}$
is at most
$\Gamma _{\mathrm{OT}}$
is at most
 $2$
larger than their distance in
$2$
larger than their distance in
 $\Gamma $
;
$\Gamma $
; -
(2) the minimal lengths of directed paths from
 $(M_{1},\xi _{1})$
to
$(M_{1},\xi _{1})$
to
 $(M_{2},\xi _{2})$
agree in
$(M_{2},\xi _{2})$
agree in
 $\Gamma $
and
$\Gamma $
and
 $\Gamma _{\mathrm{OT}}$
.
$\Gamma _{\mathrm{OT}}$
.
Proof. (1) Let p be a minimal (undirected) path between
![]() $(M_{1},\xi _{1})$
and
$(M_{1},\xi _{1})$
and
![]() $(M_{2},\xi _{2})$
in
$(M_{2},\xi _{2})$
in
![]() $\Gamma $
. If every vertex in p corresponds to an overtwisted contact manifold, the distances in
$\Gamma $
. If every vertex in p corresponds to an overtwisted contact manifold, the distances in
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _{\textrm {OT}}$
agree. In general, however, the path p might run through tight contact manifolds. To prevent this, we choose an ordered surgery link L in
$\Gamma _{\textrm {OT}}$
agree. In general, however, the path p might run through tight contact manifolds. To prevent this, we choose an ordered surgery link L in
![]() $(M_{1},\xi _{1})$
such that contact
$(M_{1},\xi _{1})$
such that contact
![]() $(\pm 1)$
-surgery in that given order along L corresponds to the path p. We denote by
$(\pm 1)$
-surgery in that given order along L corresponds to the path p. We denote by
![]() $\xi _{0}$
the overtwisted contact structure on
$\xi _{0}$
the overtwisted contact structure on
![]() $S^{3}$
with vanishing normalised
$S^{3}$
with vanishing normalised
![]() $\operatorname {\mathrm {d}}_{3}$
-invariant. A
$\operatorname {\mathrm {d}}_{3}$
-invariant. A
![]() $2$
-component surgery diagram of
$2$
-component surgery diagram of
![]() $(S^{3},\xi _{0})$
is shown in Figure 1 (centre). We add this surgery diagram in a Darboux ball in the exterior of L to the surgery link, where we first perform the surgeries along the two new Legendrian knots and afterwards the surgeries corresponding to p. Then any contact manifold in the path p is replaced by a connected sum with
$(S^{3},\xi _{0})$
is shown in Figure 1 (centre). We add this surgery diagram in a Darboux ball in the exterior of L to the surgery link, where we first perform the surgeries along the two new Legendrian knots and afterwards the surgeries corresponding to p. Then any contact manifold in the path p is replaced by a connected sum with
![]() $(S^{3},\xi _{0})$
. By Eliashberg’s classification of overtwisted contact structures [Reference Eliashberg9], it follows that we have constructed a new path
$(S^{3},\xi _{0})$
. By Eliashberg’s classification of overtwisted contact structures [Reference Eliashberg9], it follows that we have constructed a new path
![]() $p^{\prime }$
from
$p^{\prime }$
from
![]() $(M_{1},\xi _{1})$
to
$(M_{1},\xi _{1})$
to
![]() $(M_{2},\xi _{2})$
in
$(M_{2},\xi _{2})$
in
![]() $\Gamma _{\textrm {OT}}$
of length
$\Gamma _{\textrm {OT}}$
of length
![]() $2$
larger than the length of p.
$2$
larger than the length of p.

Figure 1 Contact surgery diagrams of contact structures on
![]() $S^{3}$
: left,
$S^{3}$
: left,
![]() $(S^{3},\xi _{-1})$
; centre,
$(S^{3},\xi _{-1})$
; centre,
![]() $(S^{3},\xi _{0})$
; right,
$(S^{3},\xi _{0})$
; right,
![]() $(S^{3},\xi _{1})$
[Reference Ding, Geiges and Stipsicz6, Reference Etnyre, Kegel and Onaran16].
$(S^{3},\xi _{1})$
[Reference Ding, Geiges and Stipsicz6, Reference Etnyre, Kegel and Onaran16].
(2) By Wand’s theorem [Reference Wand29], any directed path in
![]() $\Gamma $
between two overtwisted contact manifolds cannot run through a tight contact manifold (see the proof of Theorem 1.4).
$\Gamma $
between two overtwisted contact manifolds cannot run through a tight contact manifold (see the proof of Theorem 1.4).
4 Topological subgraphs of
 $\Gamma $
$\Gamma $
Before we prove Theorem 1.6, we first discuss the corresponding result for
![]() $S^{3}$
.
$S^{3}$
.
Lemma 4.1.
![]() $\Gamma _{S^{3}}$
is connected.
$\Gamma _{S^{3}}$
is connected.
Proof. Recall that, by the work of Eliashberg,
![]() $\xi _{\mathrm {st}}$
is the unique tight contact structure on
$\xi _{\mathrm {st}}$
is the unique tight contact structure on
![]() $S^{3}$
[Reference Eliashberg11] and the overtwisted contact structures are in one-to-one correspondence to the homotopy classes of tangential
$S^{3}$
[Reference Eliashberg11] and the overtwisted contact structures are in one-to-one correspondence to the homotopy classes of tangential
![]() $2$
-plane fields [Reference Eliashberg9], which are on homology spheres in bijection with the integers via their normalised
$2$
-plane fields [Reference Eliashberg9], which are on homology spheres in bijection with the integers via their normalised
![]() $\mathrm{d}_{3}$
-invariants [Reference Gompf19]. We denote the unique overtwisted contact structure on
$\mathrm{d}_{3}$
-invariants [Reference Gompf19]. We denote the unique overtwisted contact structure on
![]() $S^{3}$
with normalised
$S^{3}$
with normalised
![]() $\mathrm{d}_{3}$
-invariant equal to n by
$\mathrm{d}_{3}$
-invariant equal to n by
![]() $\xi _{n}$
.
$\xi _{n}$
.
Contact surgery diagrams for all contact structures on
![]() $S^{3}$
were explicitly described in [Reference Ding, Geiges and Stipsicz6]. A contact surgery diagram of
$S^{3}$
were explicitly described in [Reference Ding, Geiges and Stipsicz6]. A contact surgery diagram of
![]() $\xi _{1}$
is given by the contact
$\xi _{1}$
is given by the contact
![]() $(+1)$
-surgery along the Legendrian unknot with Thurston–Bennequin invariant
$(+1)$
-surgery along the Legendrian unknot with Thurston–Bennequin invariant
![]() $\mathrm{tb}=-2$
and rotation number
$\mathrm{tb}=-2$
and rotation number
![]() $\mathrm{rot}=1$
, shown on the right of Figure 1. The contact
$\mathrm{rot}=1$
, shown on the right of Figure 1. The contact
![]() $(\pm 1)$
-surgery diagram along the
$(\pm 1)$
-surgery diagram along the
![]() $2$
-component link, shown on the left of Figure 1, represents
$2$
-component link, shown on the left of Figure 1, represents
![]() $\xi _{-1}$
. The disjoint union of two surgery diagrams describes a connected sum of the underlying contact manifolds. Since the
$\xi _{-1}$
. The disjoint union of two surgery diagrams describes a connected sum of the underlying contact manifolds. Since the
![]() $\mathrm{d}_{3}$
-invariant behaves additively under the connected sum, we get contact surgery diagrams of all contact structures on
$\mathrm{d}_{3}$
-invariant behaves additively under the connected sum, we get contact surgery diagrams of all contact structures on
![]() $S^{3}$
by taking appropriate disjoint unions of the contact surgery diagrams of
$S^{3}$
by taking appropriate disjoint unions of the contact surgery diagrams of
![]() $\xi _{1}$
and
$\xi _{1}$
and
![]() $\xi _{-1}$
.
$\xi _{-1}$
.
It follows that we can get
![]() $(S^{3},\xi _{1})$
by a single contact
$(S^{3},\xi _{1})$
by a single contact
![]() $(+1)$
-surgery from
$(+1)$
-surgery from
![]() $(S^{3},\xi _{\mathrm {st}})$
and that there exists a contact
$(S^{3},\xi _{\mathrm {st}})$
and that there exists a contact
![]() $(+1)$
-surgery on
$(+1)$
-surgery on
![]() $(S^{3},\xi _{k})$
yielding
$(S^{3},\xi _{k})$
yielding
![]() $(S^{3},\xi _{k+1})$
and thus conversely a contact
$(S^{3},\xi _{k+1})$
and thus conversely a contact
![]() $(-1)$
-surgery from
$(-1)$
-surgery from
![]() $(S^{3},\xi _{k})$
to
$(S^{3},\xi _{k})$
to
![]() $(S^{3},\xi _{k-1})$
.
$(S^{3},\xi _{k-1})$
.
Proof of Theorem 1.6.
First we discuss the case that M is a homology sphere. Then we can get any overtwisted contact structure on M from a fixed contact structure on M by connected summing with overtwisted contact structures of
![]() $S^{3}$
[Reference Ding, Geiges and Stipsicz6]. It follows that any two overtwisted contact structures on M can be connected in
$S^{3}$
[Reference Ding, Geiges and Stipsicz6]. It follows that any two overtwisted contact structures on M can be connected in
![]() $\Gamma _{M}$
. Now let
$\Gamma _{M}$
. Now let
![]() $\xi _{\textrm {tight}}$
be some tight contact structure on M. Then there exists a single contact
$\xi _{\textrm {tight}}$
be some tight contact structure on M. Then there exists a single contact
![]() $(+1)$
-surgery along a Legendrian unknot in
$(+1)$
-surgery along a Legendrian unknot in
![]() $(M,\xi _{\textrm {tight}})$
yielding
$(M,\xi _{\textrm {tight}})$
yielding
![]() $(M,\xi _{\textrm {tight}})\# (S^{3},\xi _{1})$
which is overtwisted, and thus it follows that
$(M,\xi _{\textrm {tight}})\# (S^{3},\xi _{1})$
which is overtwisted, and thus it follows that
![]() $\Gamma _{M}$
is connected.
$\Gamma _{M}$
is connected.
If the underlying manifold is not a homology sphere, it gets slightly more complicated since the classification of tangential
![]() $2$
-plane fields is more involved. As a further invariant, we have the
$2$
-plane fields is more involved. As a further invariant, we have the
![]() $\mathit {spin}^{c}$
structure of a contact structure. However, it is known that for a given contact structure with
$\mathit {spin}^{c}$
structure of a contact structure. However, it is known that for a given contact structure with
![]() $\mathit {spin}^{c}$
structure
$\mathit {spin}^{c}$
structure
![]() $\mathfrak s$
, we can get any other overtwisted contact structure with the same
$\mathfrak s$
, we can get any other overtwisted contact structure with the same
![]() $\mathit {spin}^{c}$
structure
$\mathit {spin}^{c}$
structure
![]() $\mathfrak s$
by connected summing with the overtwisted contact structures on
$\mathfrak s$
by connected summing with the overtwisted contact structures on
![]() $S^{3}$
[Reference Ding, Geiges and Stipsicz6]. Thus, we can apply the same argument as in the homology sphere case to deduce that
$S^{3}$
[Reference Ding, Geiges and Stipsicz6]. Thus, we can apply the same argument as in the homology sphere case to deduce that
![]() $\Gamma _{(M,\mathfrak s)}$
is connected.
$\Gamma _{(M,\mathfrak s)}$
is connected.
It remains to show that there is no edge connecting two different
![]() $\mathit {spin}^{c}$
structures on M. For that, we use Gompf’s
$\mathit {spin}^{c}$
structures on M. For that, we use Gompf’s
![]() $\Gamma $
-invariant which classifies
$\Gamma $
-invariant which classifies
![]() $\mathit {spin}^{c}$
structures [Reference Gompf19]. Let
$\mathit {spin}^{c}$
structures [Reference Gompf19]. Let
![]() $\mathfrak s$
be a
$\mathfrak s$
be a
![]() $\mathit {spin}^{c}$
structure on M and
$\mathit {spin}^{c}$
structure on M and
![]() $\xi $
be a contact structure inducing
$\xi $
be a contact structure inducing
![]() $\mathfrak s$
. Let
$\mathfrak s$
. Let
![]() $L_{0}$
in
$L_{0}$
in
![]() $(M,\xi )$
be a Legendrian knot such that contact
$(M,\xi )$
be a Legendrian knot such that contact
![]() $(+1)$
- or contact
$(+1)$
- or contact
![]() $(-1)$
-surgery along
$(-1)$
-surgery along
![]() $L_{0}$
yields another contact structure
$L_{0}$
yields another contact structure
![]() $\xi ^{\prime }$
on M. We want to show that
$\xi ^{\prime }$
on M. We want to show that
![]() $\xi ^{\prime }$
induces the same
$\xi ^{\prime }$
induces the same
![]() $\mathit {spin}^{c}$
structure
$\mathit {spin}^{c}$
structure
![]() $\mathfrak s$
. For that, we choose a spin structure
$\mathfrak s$
. For that, we choose a spin structure
![]() $\mathfrak t$
, describe
$\mathfrak t$
, describe
![]() $(M,\xi )$
by a contact surgery diagram along a Legendrian link
$(M,\xi )$
by a contact surgery diagram along a Legendrian link
![]() $L=L_{1}\cup \cdots \cup L_{n}$
in
$L=L_{1}\cup \cdots \cup L_{n}$
in
![]() $(S^{3},\xi _{\mathrm {st}})$
and present
$(S^{3},\xi _{\mathrm {st}})$
and present
![]() $L_{0}$
as a knot in the exterior of L. To show that
$L_{0}$
as a knot in the exterior of L. To show that
![]() $\xi $
and
$\xi $
and
![]() $\xi ^{\prime }$
induce the same
$\xi ^{\prime }$
induce the same
![]() $\mathit {spin}^{c}$
structures, it is enough to compute that Gompf’s
$\mathit {spin}^{c}$
structures, it is enough to compute that Gompf’s
![]() $\Gamma $
invariants of
$\Gamma $
invariants of
![]() $\xi $
and
$\xi $
and
![]() $\xi ^{\prime }$
with respect to
$\xi ^{\prime }$
with respect to
![]() $\mathfrak t$
agree. We present
$\mathfrak t$
agree. We present
![]() $\mathfrak t$
via a characteristic sublink
$\mathfrak t$
via a characteristic sublink
![]() $(L_{j})_{j\in J}$
,
$(L_{j})_{j\in J}$
,
![]() $J\subset \{1,\ldots ,n\}$
, of L. Since the homologies of M and
$J\subset \{1,\ldots ,n\}$
, of L. Since the homologies of M and
![]() $L_{0}(\pm 1)$
agree, we deduce that
$L_{0}(\pm 1)$
agree, we deduce that
![]() $\mu _{L_{0}}$
is nullhomologous in
$\mu _{L_{0}}$
is nullhomologous in
![]() $L_{0}(\pm 1)$
and that J is also a characteristic sublink of the surgery diagram
$L_{0}(\pm 1)$
and that J is also a characteristic sublink of the surgery diagram
![]() $L_{0}\cup L$
of
$L_{0}\cup L$
of
![]() $L_{0}(\pm 1)$
. Then we can use the formula for computing Gompf’s
$L_{0}(\pm 1)$
. Then we can use the formula for computing Gompf’s
![]() $\Gamma $
-invariant from [Reference Etnyre, Kegel and Onaran16] to compute
$\Gamma $
-invariant from [Reference Etnyre, Kegel and Onaran16] to compute
 $$ \begin{align*} \Gamma(\xi^{\prime},\mathfrak t)-\Gamma(\xi,\mathfrak t)=\frac{1}{2} \bigg(\sum_{i=0}^{n} r_{i}\mu_{i}+\sum_{j\in J}(Q^{\prime}\mu)_{j}\bigg)-\frac{1}{2} \bigg(\sum_{i=1}^{n} r_{i}\mu_{i}+\sum_{j\in J}(Q\mu)_{j}\bigg)=0, \end{align*} $$
$$ \begin{align*} \Gamma(\xi^{\prime},\mathfrak t)-\Gamma(\xi,\mathfrak t)=\frac{1}{2} \bigg(\sum_{i=0}^{n} r_{i}\mu_{i}+\sum_{j\in J}(Q^{\prime}\mu)_{j}\bigg)-\frac{1}{2} \bigg(\sum_{i=1}^{n} r_{i}\mu_{i}+\sum_{j\in J}(Q\mu)_{j}\bigg)=0, \end{align*} $$
where
![]() $r_{i}$
denotes the rotation number and
$r_{i}$
denotes the rotation number and
![]() $\mu _{i}$
the meridian of
$\mu _{i}$
the meridian of
![]() $L_{i}$
,
$L_{i}$
,
![]() $Q^{\prime }$
and Q denote the linking matrices of
$Q^{\prime }$
and Q denote the linking matrices of
![]() $L_{0}\cup L$
and L, and all noncancelling terms are multiples of
$L_{0}\cup L$
and L, and all noncancelling terms are multiples of
![]() $\mu _{0}=0$
.
$\mu _{0}=0$
.
We now turn to the proof of Theorem 1.7. For the proof, we need the following lemma.
Lemma 4.2. Let L be a Legendrian knot in some contact
![]() $3$
-manifold
$3$
-manifold
![]() $(M,\xi )$
and U be a Legendrian meridian of L with
$(M,\xi )$
and U be a Legendrian meridian of L with
![]() $\operatorname {\mathrm {tb}}=-1$
. Let
$\operatorname {\mathrm {tb}}=-1$
. Let
![]() $L_{\pm }$
denote the positive/negative stabilisation of L (similarly for U). Then contact
$L_{\pm }$
denote the positive/negative stabilisation of L (similarly for U). Then contact
![]() $(-1)$
-surgery along L followed by contact
$(-1)$
-surgery along L followed by contact
![]() $(+1)$
-surgery along
$(+1)$
-surgery along
![]() $U_{\pm }$
is contactomorphic to the contact
$U_{\pm }$
is contactomorphic to the contact
![]() $(+1)$
-surgery along
$(+1)$
-surgery along
![]() $L_{\pm }$
(see Figure 2), that is,
$L_{\pm }$
(see Figure 2), that is,
![]() $L(-1)\cup U_{\pm }(+1)=L_{\pm }(+1)$
.
$L(-1)\cup U_{\pm }(+1)=L_{\pm }(+1)$
.

Figure 2 From a contact
![]() $(-1)$
-surgery to a contact
$(-1)$
-surgery to a contact
![]() $(+1)$
-surgery.
$(+1)$
-surgery.
Proof. We relate the two contact surgery diagrams in Figure 2 by first performing two handle slides [Reference Avdek1, Reference Casals, Etnyre and Kegel2, Reference Ding and Geiges5] followed by a lantern destabilisation [Reference Lisca and Stipsicz24] (see also [Reference Etnyre, Kegel and Onaran16]). We first slide the red knot L over
![]() $U_{+}$
, as in Figure 3(i). Then, we slide
$U_{+}$
, as in Figure 3(i). Then, we slide
![]() $U_{+}$
over the red one as in Figure 3(ii), where the handle slides are indicated via the arrows. After isotoping Figure 3(iii) to get Figure 3(iv), we apply the lantern destabilisation to get Figure 3(v).
$U_{+}$
over the red one as in Figure 3(ii), where the handle slides are indicated via the arrows. After isotoping Figure 3(iii) to get Figure 3(iv), we apply the lantern destabilisation to get Figure 3(v).

Figure 3 Proof of Lemma 4.2 via two handle slides and a lantern destabilisation.
Proof of Theorem 1.7.
Let
![]() $(N,\xi _{N})$
be a contact manifold in the link of
$(N,\xi _{N})$
be a contact manifold in the link of
![]() $(M,\xi )$
. We construct a path of length one or two in
$(M,\xi )$
. We construct a path of length one or two in
![]() $\operatorname {\mathrm {lk}}(M,\xi )$
from
$\operatorname {\mathrm {lk}}(M,\xi )$
from
![]() $(N,\xi _{N})$
to
$(N,\xi _{N})$
to
![]() $(M,\xi )\#(S^{3},\xi _{1})$
. (We recall that
$(M,\xi )\#(S^{3},\xi _{1})$
. (We recall that
![]() $(M,\xi )\#(S^{3},\xi _{1})$
can be obtained from
$(M,\xi )\#(S^{3},\xi _{1})$
can be obtained from
![]() $(M,\xi )$
by a single contact
$(M,\xi )$
by a single contact
![]() $(+1)$
-surgery along a Legendrian unknot with
$(+1)$
-surgery along a Legendrian unknot with
![]() $\operatorname {\mathrm {tb}}=-2$
in a standard Darboux ball in
$\operatorname {\mathrm {tb}}=-2$
in a standard Darboux ball in
![]() $(M,\xi )$
.)
$(M,\xi )$
.)
First, we consider the case in which we can obtain
![]() $(N,\xi _{N})$
by a contact
$(N,\xi _{N})$
by a contact
![]() $(+1)$
-surgery along a Legendrian knot K in
$(+1)$
-surgery along a Legendrian knot K in
![]() $(M,\xi )$
. In [Reference Avdek1] it is shown that performing a contact
$(M,\xi )$
. In [Reference Avdek1] it is shown that performing a contact
![]() $(+1)$
-surgery K followed by a contact
$(+1)$
-surgery K followed by a contact
![]() $(+1)$
-surgery along a Legendrian meridian U of K with
$(+1)$
-surgery along a Legendrian meridian U of K with
![]() $\operatorname {\mathrm {tb}}=-1$
corresponds to a negative stabilisation of
$\operatorname {\mathrm {tb}}=-1$
corresponds to a negative stabilisation of
![]() $(M,\xi )$
and thus yields
$(M,\xi )$
and thus yields
![]() $(M,\xi )\#(S^{3},\xi _{1})$
.
$(M,\xi )\#(S^{3},\xi _{1})$
.
The case in which
![]() $(N,\xi _{N})$
arises as contact
$(N,\xi _{N})$
arises as contact
![]() $(-1)$
-surgery from
$(-1)$
-surgery from
![]() $(M,\xi )$
can be reduced to the first case by applying Lemma 4.2 once.
$(M,\xi )$
can be reduced to the first case by applying Lemma 4.2 once.
The proof of Theorem 1.7 directly implies the following corollary.
Corollary 4.3.
-
(1) If
 $(N,\xi )$
is in the link of
$(N,\xi )$
is in the link of
 $(M,\xi )$
, then
$(M,\xi )$
, then  $$ \begin{align*} d_{\operatorname{\mathrm{lk}}(M,\xi)}((N,\xi),(M,\xi)\#(S^{3},\xi_{1}))\leq2. \end{align*} $$
$$ \begin{align*} d_{\operatorname{\mathrm{lk}}(M,\xi)}((N,\xi),(M,\xi)\#(S^{3},\xi_{1}))\leq2. \end{align*} $$
-
(2) If
 $(N,\xi )$
can be obtained from
$(N,\xi )$
can be obtained from
 $(M,\xi )$
by a single contact
$(M,\xi )$
by a single contact
 $(+1)$
-surgery, then
$(+1)$
-surgery, then
 $(N,\xi )$
can be obtained from
$(N,\xi )$
can be obtained from
 $(M,\xi )\#(S^{3},\xi _{1})$
by a single contact
$(M,\xi )\#(S^{3},\xi _{1})$
by a single contact
 $(-1)$
-surgery.
$(-1)$
-surgery.
Acknowledgements
M.K. thanks Chris Wendl and Felix Schmäschke for useful discussions. We would also like to thank the Mathematisches Forschungsinstitut Oberwolfach where a part of this project was carried out when M.K. was Oberwolfach Research Fellow in August 2020.