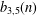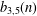Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Naika, M. S. Mahadeva
and
Harishkumar, T.
2019.
On $(4, 5)$-regular bipartitions with odd parts distinct.
Tbilisi Mathematical Journal,
Vol. 12,
Issue. 3,