No CrossRef data available.
Published online by Cambridge University Press: 29 January 2024
Ranks of partitions play an important role in the theory of partitions. They provide combinatorial interpretations for Ramanujan’s famous congruences for partition functions. We establish a family of congruences modulo powers of 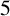 $5$ for ranks of partitions.
$5$ for ranks of partitions.
This work is supported by NSFC (National Natural Science Foundation of China) through Grant No. NSFC 12071331.