Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T02:10:34.804Z Has data issue: false hasContentIssue false
  • English
  • Français

CONDITIONAL FEYNMAN INTEGRAL AND SCHRÖDINGER INTEGRAL EQUATION ON A FUNCTION SPACE

Part of: Set functions and measures on spaces with additional structure

Published online by Cambridge University Press:  10 March 2009

DONG HYUN CHO
DONG HYUN CHO*
Affiliation:
Department of Mathematics, Kyonggi University, Kyonggido Suwon 443-760, Korea (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Cr[0,t] be the function space of the vector-valued continuous paths x:[0,t]→ℝr and define Xt:Cr[0,t]→ℝ(n+1)r by Xt(x)=(x(0),x(t1),…,x(tn)), where 0<t1<⋯<tn=t. In this paper, using a simple formula for the conditional expectations of the functions on Cr[0,t] given Xt, we evaluate the conditional analytic Feynman integral Eanfq[Ft∣Xt] of Ft given by 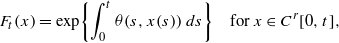where θ(s,⋅) are the Fourier–Stieltjes transforms of the complex Borel measures on ℝr, and provide an inversion formula for Eanfq[Ft∣Xt]. Then we present an existence theorem for the solution of an integral equation including the integral equation which is formally equivalent to the Schrödinger differential equation. We show that the solution can be expressed by Eanfq[Ft∣Xt] and a probability distribution on ℝr when Xt(x)=(x(0),x(t)).

Keywords

analytic Feynman integralconditional analytic Feynman integralSchrödinger equationtime-dependent potentialWiener space

MSC classification

Secondary: 28C20: Set functions and measures and integrals in infinite-dimensional spaces (Wiener measure, Gaussian measure, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 1 , February 2009 , pp. 1 - 22
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

This work was supported by Kyonggi University Research Grant.

References

[1] Cameron, R. H. and Storvick, D. A., Some Banach Algebras of Analytic Feynman Integrable Functionals, Lecture Notes in Mathematics, 798 (Springer, Berlin, 1980).CrossRefGoogle Scholar
[2] Cameron, R. H. and Storvick, D. A., ‘Analytic Feynman integral solutions of an integral equation related to the Schrödinger equation’, J. Analyse Math. 38 (1980), 34–66.CrossRefGoogle Scholar
[3] Cameron, R. H. and Storvick, D. A., ‘An operator valued function space integral and a related integral equation’, J. Math. Mech. 18(6) (1968), 517–552.Google Scholar
[4] Cho, D. H., ‘A simple formula for an analogue of conditional Wiener integrals and its applications’, Trans. Amer. Math. Soc. 360(7) (2008), 3795–3811.Google Scholar
[5] Chung, D. M. and Kang, S. H., ‘Conditional Feynman integrals involving indefinite quadratic form’, J. Korean Math. Soc. 31(3) (1994), 521–537.Google Scholar
[6] Chung, D. M., Kang, S. H. and Kang, S. J., ‘A class of conditional analytic Feynman integrals’, Commun. Korean Math. Soc. 11(1) (1996), 175–190.Google Scholar
[7] Chung, D. M. and Skoug, D. L., ‘Conditional analytic Feynman integrals and a related Schrödinger integral equation’, SIAM J. Math. Anal. 20(4) (1989), 950–965.Google Scholar
[8] Im, M. K. and Ryu, K. S., ‘An analogue of Wiener measure and its applications’, J. Korean Math. Soc. 39(5) (2002), 801–819.Google Scholar
[9] Johnson, G. W. and Skoug, D. L., ‘Notes on the Feynman integral, III: The Schroedinger equation’, Pacific J. Math. 105(2) (1983), 321–358.CrossRefGoogle Scholar
[10] Park, C. and Skoug, D. L., ‘A simple formula for conditional Wiener integrals with applications’, Pacific J. Math. 135(2) (1988), 381–394.CrossRefGoogle Scholar
[11] Ryu, K. S. and Im, M. K., ‘A measure-valued analogue of Wiener measure and the measure-valued Feynman–Kac formula’, Trans. Amer. Math. Soc. 354(12) (2002), 4921–4951.CrossRefGoogle Scholar