Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-09T09:32:35.409Z Has data issue: false hasContentIssue false
  • English
  • Français

The computational complexity of torsion-freeness of finitely presented groups

Published online by Cambridge University Press:  17 April 2009

Steffen Lempp
Steffen Lempp
Affiliation:
Department of MathematicsUniversity of WisoncsinMadison WI 53706–1388United States of America email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

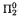We determine the complexity of torsion-freeness of finitely presented groups in Kleene's arithmetical hierarchy as -complete. This implies in particular that there is no effective listing of all torsion-free finitely presented groups, or of all non-torsion-free finitely presented groups.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 56 , Issue 2 , October 1997 , pp. 273 - 277
Copyright
Copyright © Australian Mathematical Society 1997

References

[1]Adian, S.I., ‘The unsolvability of certain algorithmic problems in the theory of groups’, Trudy Moskov. Mat. Obshch. 6 (1957), 231–298.Google Scholar
[2]Adian, S.I., ‘Finitely presented groups and algorithms’, Dokl. Akad. Nauk SSSR 117 (1957), 9–12.Google Scholar
[3]Baumslag, G., Boone, W.W. and Neumann, B.H., ‘Some unsolvable problems about elements and subgroups of groups’, Math. Scand. 7 (1959), 191–201.CrossRefGoogle Scholar
[4]Boone, W.W., ‘Certain simple unsolvable problems in group theory I’, Nederl. Akad. Wetensch. Proc. Ser. A 57 (1954), 231–237. ‘II’, Nederl. Akad. Wetensch. Proc. Ser. A 57 (1954), 492–497. ‘III’, Nederl. Akad. Wetensch. Proc. Ser. A 58 (1955), 252–256. ‘IV’, Nederl. Akad. Wetensch. Proc. Ser. A 58 (1955), 571–577. ‘V’, Nederl. Akad. Wetensch. Proc. Ser. A 60 (1957), 22–27. ‘VI’, Nederl. Akad. Wetensch. Proc. Ser. A 60 (1957), 227–232.CrossRefGoogle Scholar
[5]Boone, W.W. and Rogers, H. Jr, ‘On a problem of J.H.C. Whitehead and a problem of Alonzo Church’, Math. Scand. 19 (1966), 185–192.CrossRefGoogle Scholar
[6]Novikov, P.S., S, P.., ‘On the algorithmic unsolvability of the word problem in group theory’, Trudy Mat. Inst. Steklov 44 (1955), 1–143.Google Scholar
[7]Rabin, M.O., ‘Recursive unsolvability of group theoretic problems’, Ann. Math. 67 (1958), 172–194.CrossRefGoogle Scholar
[8]Rotman, J.J., An introduction to the theory of groups (Springer-Verlag, Berlin, Heidelberg, New York, 1995).CrossRefGoogle Scholar
[9]Soare, R.I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets (Springer-Verlag, Berlin, Heidelberg, New York, 1987).CrossRefGoogle Scholar