Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stević, Stevo
and
Sharma, Ajay K.
2011.
Essential norm of composition operators between weighted Hardy spaces.
Applied Mathematics and Computation,
Vol. 217,
Issue. 13,
p.
6192.
Sharma, Ajay K.
2012.
Generalized composition operators between Hardy and weighted Bergman spaces.
Acta Scientiarum Mathematicarum,
Vol. 78,
Issue. 1-2,
p.
187.
Sehba, Benoît
and
Stević, Stevo
2014.
On some product-type operators from Hardy–Orlicz and Bergman–Orlicz spaces to weighted-type spaces.
Applied Mathematics and Computation,
Vol. 233,
Issue. ,
p.
565.
Abbas, Zaheer
and
Magotra, Sonali
2020.
Sandwich weighted composition operators between some families of analytic functions.
Advances in Operator Theory,
Vol. 5,
Issue. 4,
p.
1434.
Guo, Zhitao
2023.
On an Extension of Stević–Sharma Operator from Weighted Bergman–Orlicz Space to Weighted-Type Space on the Unit Ball.
Complex Analysis and Operator Theory,
Vol. 17,
Issue. 1,
Zhou, Hang
and
Kavallaris, Nikos
2024.
Weighted composition operators on the logarithmic Bloch-Orlicz space.
PLOS ONE,
Vol. 19,
Issue. 5,
p.
e0303336.


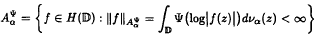
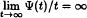 . In fact, under a mild condition on ∞, we show that every holomorphic-self map ∞ of
. In fact, under a mild condition on ∞, we show that every holomorphic-self map ∞ of 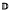 induces a bounded composition operator on
induces a bounded composition operator on 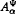 and
and  .
.