Published online by Cambridge University Press: 24 June 2021
For any (Hausdorff) compact group G, denote by
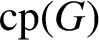 $\mathrm{cp}(G)$
the probability that a randomly chosen pair of elements of G commute. We prove that there exists a finite group H such that
$\mathrm{cp}(G)$
the probability that a randomly chosen pair of elements of G commute. We prove that there exists a finite group H such that
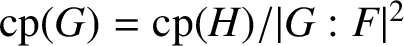 $\mathrm{cp}(G)= {\mathrm{cp}(H)}/{|G:F|^2}$
, where F is the FC-centre of G and H is isoclinic to F with
$\mathrm{cp}(G)= {\mathrm{cp}(H)}/{|G:F|^2}$
, where F is the FC-centre of G and H is isoclinic to F with
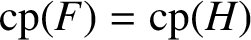 $\mathrm{cp}(F)=\mathrm{cp}(H)$
whenever
$\mathrm{cp}(F)=\mathrm{cp}(H)$
whenever
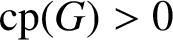 $\mathrm{cp}(G)>0$
. In addition, we prove that a compact group G with
$\mathrm{cp}(G)>0$
. In addition, we prove that a compact group G with
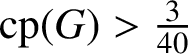 $\mathrm{cp}(G)>\tfrac {3}{40}$
is either solvable or isomorphic to
$\mathrm{cp}(G)>\tfrac {3}{40}$
is either solvable or isomorphic to
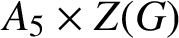 $A_5 \times Z(G)$
, where
$A_5 \times Z(G)$
, where
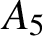 $A_5$
denotes the alternating group of degree five and the centre
$A_5$
denotes the alternating group of degree five and the centre
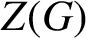 $Z(G)$
of G contains the identity component of G.
$Z(G)$
of G contains the identity component of G.
The research of the second author was in part supported by a grant from the Institute for Research in Fundamental Sciences (IPM) (No. 1400200043). This research was supported in part by a grant from School of Mathematics, Institute for Research in Fundamental Sciences.