Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-27T12:35:24.442Z Has data issue: false hasContentIssue false
  • English
  • Français

COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK

Part of: Connections with homological algebra and category theory Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  16 February 2012

KARL LORENSEN
KARL LORENSEN*
Affiliation:
Altoona College, Pennsylvania State University, Altoona, PA 16601, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that G is a solvable group whose elementary abelian sections are all finite. Suppose, further, that p is a prime such that G fails to contain any subgroups isomorphic to Cp∞. We show that if G is nilpotent, then the pro-p completion map 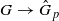induces an isomorphism 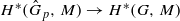for any discrete 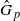-module M of finite p-power order. For the general case, we prove that G contains a normal subgroup N of finite index such that the map 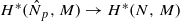is an isomorphism for any discrete 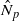-module M of finite p-power order. Moreover, if G lacks any Cp∞-sections, the subgroup N enjoys some additional special properties with respect to its pro-p topology.

Keywords

solvable groupsnilpotent groupsprofinite completionspro-p completionsprofinite topologypro-p topologySerre’s good groups

MSC classification

Secondary: 20F16: Solvable groups, supersolvable groups 20J06: Cohomology of groups 20E18: Limits, profinite groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 86 , Issue 2 , October 2012 , pp. 254 - 265
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2012

References

[1]Cutolo, G. and Smith, H., ‘A note on polycyclic residually finite-p groups’, Glasg. Math. J. 52(1) (2010), 137–143.CrossRefGoogle Scholar
[2]Kropholler, P., Private communication.Google Scholar
[3]Lennox, J. and Robinson, D., The Theory of Infinite Soluble Groups (Clarendon Press, Oxford, 2004).CrossRefGoogle Scholar
[4]Linnell, P. and Schick, T., ‘Finite group extensions and the Atiyah conjecture’, J. Amer. Math. Soc. 20 (2007), 1003–1051.CrossRefGoogle Scholar
[5]Robinson, D., ‘On the cohomology of soluble groups of finite rank’, J. Pure Appl. Algebra 6 (1975), 155–164.CrossRefGoogle Scholar
[6]Serre, J.-P., Galois Cohomology (Springer, Berlin, 1997).CrossRefGoogle Scholar
[7]S̆mel’kin, A., ‘Polycyclic groups’, Sibirsk Mat. Zh. 9 (1968), 234–235.Google Scholar
[8]Weigel, T., ‘On profinite groups with finite abelianizations’, Selecta Math. (N.S.) 13 (2007), 175–181.CrossRefGoogle Scholar