Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T06:19:56.656Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficient estimates for alpha-spiral functions

Published online by Cambridge University Press:  17 April 2009

B.L. Bhatia  and
S. Rajasekaran
B.L. Bhatia
Affiliation:
Department of Mathematics, Indian Institute of Technology Kanpur, IIT Post Office, Kanpur - 208016, U.P., India.
S. Rajasekaran
Affiliation:
Department of Mathematics, Indian Institute of Technology Kanpur, IIT Post Office, Kanpur - 208016, U.P., India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 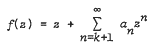belong to the class of α-spiral functions of order ρ(|α| < π/2, 0 ≤ ρ < 1). In this paper, we determine sharp coefficient estimates for functions of the form f(z)t, where t is a positive integer. We also study the influence of the second coefficient on the other coefficients for such functions. The results obtained not only generalize the results of MacGregor, Boyd, Srivastava, Silverman and Silvia and others, but also give rise to new results.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 28 , Issue 3 , December 1983 , pp. 319 - 329
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Boyd, A.V., “Coefficient estimates for starlike functions of order α”, Proc. Amer. Math. Soc. 17 (1966), 1016–1019.Google Scholar
[2]Goluzin, G.M., “On some estimates for functions which map the circle conformally and univalently” (Russian), Recueil Math. Moscow 36 (1929), 152–172.Google Scholar
[3]Libera, R.J., “Univalent α–spiral functions”, Canad. J. Math. 19 (1967), 449–456.CrossRefGoogle Scholar
[4]MacGregor, T.H., “Coefficient estimates for mappings”, Michigan Math. J. 10 (1963), 277–281.Google Scholar
[5]Silverman, H. and Silvia, E.M., “The influence of the second coefficient on prestarlike functions”, Rocky Mountain J. Math. 10 (1980), 469–474.Google Scholar
[6]Špaček, L., “Contributions à la théorie des fonctions univalents” (Czech.), Časopes. Pěst. Mat. 62 (1963), 12–19.Google Scholar
[7]Srivastava, R.S.L., “Univalent spiral functions”, Topics in analysis, 327–341 (Lecture Notes in Mathematics, 419. Springer-Verlag, Berlin, Heidelberg, New York, 1974).Google Scholar
[8]Zamorski, J., “About the extremal spiral Schlicht functions”, Ann. Polon. Math. 9 (1960/1961), 265–273.Google Scholar