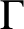A graph $\Gamma $ is called 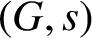$(G, s)$ -arc-transitive if 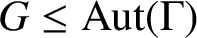$G \le \text{Aut} (\Gamma )$ is transitive on the set of vertices of $\Gamma $ and the set of s-arcs of 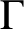$\Gamma $ , where for an integer 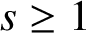$s \ge 1$ an s-arc of 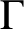$\Gamma $ is a sequence of 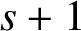$s+1$ vertices 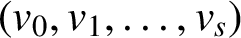$(v_0,v_1,\ldots ,v_s)$ of 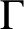$\Gamma $ such that 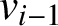$v_{i-1}$ and 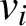$v_i$ are adjacent for $1 \le i \le s$ and 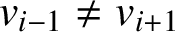$v_{i-1}\ne v_{i+1}$ for 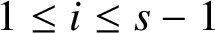$1 \le i \le s-1$ . 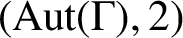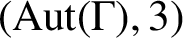A graph $\Gamma $ is called 2-transitive if it is $(\text{Aut} (\Gamma ), 2)$ -arc-transitive but not $(\text{Aut} (\Gamma ), 3)$ -arc-transitive. A Cayley graph 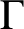$\Gamma $ of a group G is called normal if G is normal in 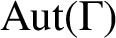$\text{Aut} (\Gamma )$ and nonnormal otherwise. Fang et al. [‘On edge transitive Cayley graphs of valency four’, European J. 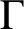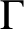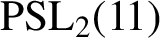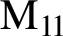Combin.25 (2004), 1103–1116] proved that if $\Gamma $ is a tetravalent 2-transitive Cayley graph of a finite simple group G, then either $\Gamma $ is normal or G is one of the groups $\text{PSL}_2(11)$ , ${\rm M} _{11}$ , 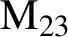$\text{M} _{23}$ and 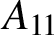$A_{11}$ . However, it was unknown whether 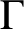$\Gamma $ is normal when G is one of these four groups. We answer this question by proving that among these four groups only 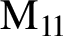$\text{M} _{11}$ produces connected tetravalent 2-transitive nonnormal Cayley graphs. We prove further that there are exactly two such graphs which are nonisomorphic and both are determined in the paper. As a consequence, the automorphism group of any connected tetravalent 2-transitive Cayley graph of any finite simple group is determined.