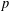Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T00:54:41.090Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSIFICATION OF REFLECTION SUBGROUPS MINIMALLY CONTAINING $p$-SYLOW SUBGROUPS

Part of: Representation theory of groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  04 October 2017

KANE DOUGLAS TOWNSEND Open the ORCID record for KANE DOUGLAS TOWNSEND [Opens in a new window]
KANE DOUGLAS TOWNSEND*
Affiliation:
Sydney, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a prime 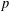$p$ divide the order of a finite real reflection group. We classify the reflection subgroups up to conjugacy that are minimal with respect to inclusion, subject to containing a 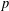$p$-Sylow subgroup. For Weyl groups, this is achieved by an algorithm inspired by the Borel–de Siebenthal algorithm. The cases where there is not a unique conjugacy class of reflection subgroups minimally containing the 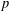$p$-Sylow subgroups are the groups of type 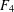$F_{4}$ when 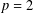$p=2$ and 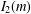$I_{2}(m)$ when 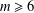$m\geq 6$ is even but not a power of 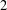$2$ for each odd prime divisor 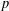$p$ of 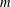$m$. The classification significantly reduces the cases required to describe the 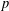$p$-Sylow subgroups of finite real reflection groups.

Keywords

finite Coxeter groupsreflection subgroupsp-Sylow subgroupsWeyl groups

MSC classification

Primary: 20F55: Reflection and Coxeter groups
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 57 - 68
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Achar, P. N., Henderson, A., Juteau, D. and Riche, S., ‘Modular generalised Springer correspondence III: exceptional groups’, Math. Ann. (2017), to appear, doi:10.1007/s00208-017-1524-4.CrossRefGoogle Scholar
Borel, A. and De Siebenthal, J., ‘Les sous-groupes fermés de rang maximum des groupes de Lie clos’, Comment. Math. Helv. 23 (1949), 200–221.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXIV. Groupes et algébres de Lie: Chapitre IV: Groupes de Coxeter et systèmes de Tits, Chapitre V: Groupes engendrés par des réflexions, Chapitre VI: systèmes de racines, Actualités Scientifiques et Industrielles, No. 1337 (Hermann, Paris, 1968).Google Scholar
Carter, R. W., ‘Conjugacy classes in the Weyl group’, Compos. Math. 25 (1972), 1–59.Google Scholar
Douglass, J. M., Pfeiffer, G. and Röhrle, G., ‘On reflection subgroups of finite Coxeter groups’, Comm. Algebra 41(7) (2013), 2574–2592.CrossRefGoogle Scholar
Dyer, M. J. and Lehrer, G. I., ‘Reflection subgroups of finite and affine Weyl groups’, Trans. Amer. Math. Soc. 363(11) (2011), 5971–6005.CrossRefGoogle Scholar
Dynkin, E. B., ‘Semisimple subalgebras of semisimple Lie algebras’, Amer. Math. Soc. Transl. Ser. 2 6 (1957), 111–244.Google Scholar
Humphreys, J. E., Reflection Groups and Coxeter Groups, Cambridge Studies in Advanced Mathematics, 29 (Cambridge University Press, Cambridge, 1997).Google Scholar
Kane, R., Reflection Groups and Invariant Theory, CMS Books in Mathematics, Ouvrages de Mathématiques de la SMC, 5 (Springer, New York, 2001).CrossRefGoogle Scholar