Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T01:20:09.605Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSIFICATION OF CUBIC HOMOGENEOUS POLYNOMIAL MAPS WITH JACOBIAN MATRICES OF RANK TWO

Part of: Affine geometry

Published online by Cambridge University Press:  30 May 2018

MICHIEL DE BONDT  and
XIAOSONG SUN Open the ORCID record for XIAOSONG SUN [Opens in a new window]
MICHIEL DE BONDT
Affiliation:
Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen, The Netherlands email [email protected]
XIAOSONG SUN*
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 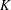$K$ be any field with 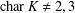$\text{char}\,K\neq 2,3$. We classify all cubic homogeneous polynomial maps 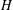$H$ over 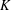$K$ whose Jacobian matrix, 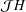${\mathcal{J}}H$, has 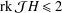$\text{rk}\,{\mathcal{J}}H\leq 2$. In particular, we show that, for such an 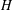$H$, if 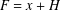$F=x+H$ is a Keller map, then 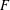$F$ is invertible and furthermore $F$ is tame if the dimension $n\neq 4$.

Keywords

cubic homogeneous polynomial mapJacobian conjectureKeller maprank-two maptame map

MSC classification

Primary: 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem)
Secondary: 14R15: Jacobian problem
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 89 - 101
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author has been supported by the Netherlands Organisation of Scientific Research (NWO). The second author has been partially supported by the NSF of China (grant nos. 11771176 and 11601146) and by the China Scholarship Council.

References

Bass, H., Connel, E. and Wright, D., ‘The Jacobian conjecture: reduction of degree and formal expansion of the inverse’, Bull. Amer. Math. Soc. 7 (1982), 287–330.CrossRefGoogle Scholar
de Bondt, M., Homogeneous Keller Maps, PhD Thesis, University of Nijmegen, Nijmegen, The Netherlands, 2009.Google Scholar
de Bondt, M., ‘Mathieu subspaces of codimension less than n of Mat n (K)’, Linear Multilinear Algebra 64(10) (2016), 2049–2067.CrossRefGoogle Scholar
de Bondt, M., ‘Rational maps H for which K (tH) has transcendence degree 2 over K ’, J. Pure Appl. Algebra (to appear), doi:10.1016/j.jpaa.2018.01.003.Google Scholar
de Bondt, M., ‘Quadratic polynomial maps with Jacobian rank two’, Preprint, 2017, arXiv:1061.00579v4 [math.AC].Google Scholar
de Bondt, M. and van den Essen, A., ‘The Jacobian conjecture: linear triangularization for homogeneous polynomial maps in dimension three’, J. Algebra 294(1) (2005), 294–306.CrossRefGoogle Scholar
de Bondt, M. and Yan, D., ‘Triangularization properties of power linear maps and the structural conjecture’, Ann. Polon. Math. 112(3) (2014), 247–266.CrossRefGoogle Scholar
van den Essen, A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathematics, 190 (Birkhäuser, Basel–Boston–Berlin, 2000).CrossRefGoogle Scholar
Hubbers, E., The Jacobian Conjecture: Cubic Homogeneous Maps in Dimension Four, Master’s Thesis, University of Nijmegen, Nijmegen, The Netherlands, 1994.Google Scholar
Jung, H., ‘Über ganze birationale Transformationen der Ebene’, J. reine angew. Math. 184 (1942), 161–174.CrossRefGoogle Scholar
van der Kulk, W., ‘On polynomial rings in two variables’, Nieuw Arch. Wiskd. 3(1) (1953), 33–41.Google Scholar
Meisters, G. and Olech, C., ‘Strong nilpotence holds in dimensions up to five only’, Linear Multilinear Algebra 30(4) (1991), 231–255.CrossRefGoogle Scholar
Pandey, A., Saxena, N. and Sinhababu, A., ‘Algebraic independence over positive characteristic: new criterion and applications to locally low algebraic rank circuits’, in: 41st Int. Symp. Mathematical Foundations of Computer Science, 2016 (eds. Sankowski, P. et al. ) (Schloss Dagstuhl, Saarbrücken, Germany, 2016), 74:1–74:15.Google Scholar
Shestakov, I. P. and Umirbaev, U. U., ‘The tame and the wild automorphisms of polynomial rings in three variables’, J. Amer. Math. Soc. 17(1) (2004), 197–227.CrossRefGoogle Scholar
Smith, M. K., ‘Stably tame automorphisms’, J. Pure Appl. Algebra 58(2) (1989), 209–212.CrossRefGoogle Scholar
Sun, X., ‘On quadratic homogeneous quasi-translations’, J. Pure Appl. Algebra 214(11) (2010), 1962–1972.CrossRefGoogle Scholar
Sun, X., ‘Classification of quadratic homogeneous automorphisms in dimension five’, Comm. Algebra 42(7) (2014), 2821–2840.CrossRefGoogle Scholar