Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T16:06:52.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of one-relator groups with centre

Published online by Cambridge University Press:  17 April 2009

James McCool
James McCool
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, CanadaM5S 1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let the group H have presentation 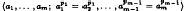where m ≥ 3, pi ≥ 2 and (pi, pj) = 1 if i ≠ j. We show that H is a one-relator group precisely if H can be obtained from a suitable group 〈a, b; ap = bp〉 by repeated applications of a (two-stage) procedure consisting of applying central Nielsen transformations followed by adjoining a root of a generator. We conjecture that any one-relator group G with non-trivial centre and G/G′ not free abelian of rank two can be obtained in the same way from a suitable group 〈a, b; ap = bp〉.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 44 , Issue 2 , October 1991 , pp. 245 - 252
Copyright
Copyright © Australian Mathematical Society 1991

References

[1]Baumslag, G. and Taylor, T., ‘The center of groups with one defining relator’, Math. Ann. 175 (1968), 315–319.CrossRefGoogle Scholar
[2]Brown, K.S., Cohomology of groups (Springer-Verlag, Berlin, Heidelberg, New York, 1982).CrossRefGoogle Scholar
[3]Collins, D.J., ‘Generation and presentation of one-relator groups with centre’, Math. Z. 157 (1978), 63–77.CrossRefGoogle Scholar
[4]Collins, D.J., ‘Presentations of the amalgamated free product of two infinite cycles’, Math. Ann. 237 (1978), 233–241.CrossRefGoogle Scholar
[5]Karrass, A., Pietrowski, A. and Solitar, D., ‘Finite and infinite cyclic extensions of free groups’, J. Austral. Math. Soc. 16 (1973), 458–466.CrossRefGoogle Scholar
[6]Magnus, W., Karrass, A., and Solitar, D., Combinatorial group theory (Interscience, New York, 1966).Google Scholar
[7]Meskin, S., Pietrowski, A. and Steinberg, A., ‘One-relator groups with center’, J. Austral. Math. Soc. 16 (1973), 319–323.CrossRefGoogle Scholar
[8]Murasugi, K., ‘The center of a group with a single defining relation’, Math. Ann. 155 (1964), 246–251.CrossRefGoogle Scholar
[9]Pietrowski, A., ‘The isomorphism problem for one-relator groups with non-trivial centre’, Math. Z. 136 (1974), 95–106.CrossRefGoogle Scholar
[10]Zieschang, H., ‘Generators of the free product with amalgamation of two infinite cyclic groups’, Math. Ann. 227 (1977), 195–221.CrossRefGoogle Scholar