Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Songxiao
and
Hasi, Wulan
2010.
Some New Characterizations of Bloch Spaces.
Taiwanese Journal of Mathematics,
Vol. 14,
Issue. 6,
Hu, Bingyang
and
Li, Songxiao
2020.
𝒩(p, q, s)-type spaces in the unit ball of ℂ
n
(II):
Carleson measure and its application.
Forum Mathematicum,
Vol. 32,
Issue. 1,
p.
79.
Shammaky, Amnah E.
Ahmed, A. El-Sayed
and
Ravichandran, V.
2022.
Characterizations of Integral Type for Weighted Classes of Analytic Banach Function Spaces.
Journal of Mathematics,
Vol. 2022,
Issue. 1,


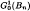 , a subspace of the Hardy space
, a subspace of the Hardy space 