Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-03T05:01:04.226Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERISATION OF THE FOURIER TRANSFORM ON COMPACT GROUPS

Part of: Compact groups Abstract harmonic analysis

Published online by Cambridge University Press:  13 November 2015

N. SHRAVAN KUMAR  and
S. SIVANANTHAN
N. SHRAVAN KUMAR*
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Delhi-110016, India email [email protected]
S. SIVANANTHAN
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Delhi-110016, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 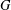$G$ be a compact group. The aim of this note is to show that the only continuous *-homomorphism from 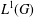$L^{1}(G)$ to 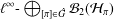$\ell ^{\infty }\text{-}\bigoplus _{[{\it\pi}]\in {\hat{G}}}{\mathcal{B}}_{2}({\mathcal{H}}_{{\it\pi}})$ that transforms a convolution product into a pointwise product is, essentially, a Fourier transform. A similar result is also deduced for maps from 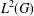$L^{2}(G)$ to 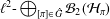$\ell ^{2}\text{-}\bigoplus _{[{\it\pi}]\in {\hat{G}}}{\mathcal{B}}_{2}({\mathcal{H}}_{{\it\pi}})$.

Keywords

compact groupsgroup Fourier transform

MSC classification

Primary: 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc.
Secondary: 22C05: Compact groups 43A32: Other transforms and operators of Fourier type 43A77: Analysis on general compact groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 3 , June 2016 , pp. 467 - 472
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alesker, S., Artstein-Avidan, S. and Milman, V., ‘A characterization of the Fourier transform and related topics’, C. R. Math. Acad. Sci. Paris 346 (2008), 625–628.Google Scholar
Alesker, S., Artstein-Avidan, S. and Milman, V., ‘A characterization of the Fourier transform and related topics’, in: Linear and Complex Analysis: Dedicated to V. P. Havin on the Occasion of his 75th Birthday, Advances in the Mathematical Sciences, American Mathematical Society Translations Series 2, 226 (American Mathematical Society, Providence, RI, 2009), 11–26.Google Scholar
Folland, G. B., A Course in Abstract Harmonic Analysis (CRC Press, Boca Raton, FL, 1995).Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. II: Structure and Analysis of Compact Groups. Analysis on Locally Compact Abelian Groups, Grundlehren der Mathematischen Wissenschaften, 152 (Springer, Berlin, 1970).Google Scholar
Jaming, P., ‘A characterization of Fourier transforms’, Colloq. Math. 118 (2010), 569–580.CrossRefGoogle Scholar
Lakshmi Lavanya, R. and Thangavelu, S., ‘A characterization of the Fourier transform on the Heisenberg group’, Ann. Funct. Anal. 3 (2012), 109–120.Google Scholar