Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saidi, Fathi B.
2002.
An Extension of the Notion of Orthogonality to Banach Spaces.
Journal of Mathematical Analysis and Applications,
Vol. 267,
Issue. 1,
p.
29.
Saidi, Fathi B.
2002.
Explicit characterizations of orthogonality in lSp(C).
Journal of Mathematical Analysis and Applications,
Vol. 271,
Issue. 2,
p.
493.
Alonso, Javier
Martini, Horst
and
Wu, Senlin
2012.
On Birkhoff orthogonality and isosceles orthogonality in normed linear spaces.
Aequationes mathematicae,
Vol. 83,
Issue. 1-2,
p.
153.
Sain, Debmalya
Paul, Kallol
and
Debnath, Lokenath
2015.
Characterization of Inner Product Spaces.
International Journal of Applied and Computational Mathematics,
Vol. 1,
Issue. 4,
p.
599.
Rahmani Jafarbeigi, R.
and
Mazaheri, H.
2020.
The Farthest Orthogonality, Best Proximity Points and Remotest Points in Banach Spaces.
Iranian Journal of Science and Technology, Transactions A: Science,
Vol. 44,
Issue. 1,
p.
195.
Astashkin, Sergei Vladimirovich
and
Semenov, Evgenii Mikhailovich
2021.
Об ортогональности в несепарабельных перестановочно-инвариантных пространствах.
Математический сборник,
Vol. 212,
Issue. 11,
p.
55.
Astashkin, S. V.
and
Semenov, E. M.
2021.
Orthogonality in nonseparable rearrangement-invariant spaces.
Sbornik: Mathematics,
Vol. 212,
Issue. 11,
p.
1553.


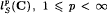 , where
, where 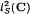 , via inner products, are obtained.
, via inner products, are obtained.