Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goldman, Mikhail L.
2011.
Some constructive criteria of optimal embeddings for potentials.
Complex Variables and Elliptic Equations,
Vol. 56,
Issue. 10-11,
p.
885.
Gogatishvili, A.
and
Stepanov, V. D.
2012.
Operators on cones of monotone functions.
Doklady Mathematics,
Vol. 86,
Issue. 1,
p.
562.
Gogatishvili, A.
Mustafayev, R. CH.
and
Persson, L.-E.
2012.
Some New Iterated Hardy-Type Inequalities.
Journal of Function Spaces and Applications,
Vol. 2012,
Issue. ,
p.
1.
Gogatishvili, A
and
Stepanov, V D
2013.
Reduction theorems for weighted integral inequalities on the cone of monotone functions.
Russian Mathematical Surveys,
Vol. 68,
Issue. 4,
p.
597.
Chen, Jianqing
and
Rocha, Eugénio M.
2013.
Advances in Harmonic Analysis and Operator Theory.
p.
123.
Arendarenko, L. S.
Oinarov, R.
and
Persson, L.-E.
2013.
Advances in Harmonic Analysis and Operator Theory.
p.
77.
Гогатишвили, Амиран
Gogatishvili, Amiran
Степанов, Владимир Дмитриевич
and
Stepanov, Vladimir Dmitrievich
2013.
Редукционные теоремы для весовых интегральных неравенств на конусе монотонных функций.
Успехи математических наук,
Vol. 68,
Issue. 4(412),
p.
3.
Gogatishvili, Amiran
Mustafayev, Rza
and
Persson, Lars-Erik
2013.
Some new iterated Hardy-type inequalities: the case "Equation missing" .
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Gogatishvili, Amiran
and
Stepanov, Vladimir D.
2013.
Reduction theorems for operators on the cones of monotone functions.
Journal of Mathematical Analysis and Applications,
Vol. 405,
Issue. 1,
p.
156.
Gogatishvili, Amiran
Moura, Susana D.
Neves, Júlio S.
and
Opic, Bohumír
2015.
Embeddings of Sobolev-type spaces into generalized Hölder spaces involving
$$k$$
k
-modulus of smoothness.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 194,
Issue. 2,
p.
425.
Křepela, Martin
2017.
Iterating Bilinear Hardy Inequalities.
Proceedings of the Edinburgh Mathematical Society,
Vol. 60,
Issue. 4,
p.
955.
Karshygina, Gulden Zh.
2017.
Optimal embeddings of Bessel and Riesz type potentials on the basis of weighted Lorentz spaces.
Vol. 1880,
Issue. ,
p.
030014.
Gogatishvili, Amiran
Mihula, Zdeněk
Pick, Luboš
Turčinová, Hana
and
Ünver, Tuğçe
2022.
Weighted Inequalities for a Superposition of the Copson Operator and the Hardy Operator.
Journal of Fourier Analysis and Applications,
Vol. 28,
Issue. 2,
Bakhtigareeva, Elza Gizarovna
and
Goldman, Mikhail L'vovich
2025.
О связи вложений и накрываний конусов функций.
Математический сборник,
Vol. 216,
Issue. 3,
p.
26.
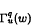 . In our proof we use a technique of discretisation and anti-discretisation developed by A. Gogatishvili and L. Pick, where they considered the opposite embedding.
. In our proof we use a technique of discretisation and anti-discretisation developed by A. Gogatishvili and L. Pick, where they considered the opposite embedding.