Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T16:44:43.414Z Has data issue: false hasContentIssue false
  • English
  • Français

A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS

Part of: Ring extensions and related topics Special categories

Published online by Cambridge University Press:  06 March 2017

WAGNER CORTES  and
THAÍSA TAMUSIUNAS
WAGNER CORTES
Affiliation:
Instituto de Matemática, Universidade Federal do Rio Grande do Sul, Porto Alegre-RS, Av. Bento Gonçalves, 9500, 91509-900, Brazil email [email protected]
THAÍSA TAMUSIUNAS*
Affiliation:
Departamento de Ciências Exatas e Sociais Aplicadas, Universidade Federal de Ciências da Saúde de Porto Alegre, Porto Alegre-RS, Rua Sarmento Leite, 245, 90050-170, Brazil email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 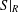$S|_{R}$ be a groupoid Galois extension with Galois groupoid 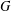$G$ such that 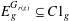$E_{g}^{G_{r(g)}}\subseteq C1_{g}$, for all 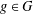$g\in G$, where 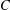$C$ is the centre of 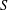$S$, $G_{r(g)}$ is the principal group associated to 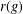$r(g)$ and $\{E_{g}\}_{g\in G}$ are the ideals of 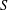$S$. We give a complete characterisation in terms of a partial isomorphism groupoid for such extensions, showing that 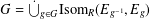$G=\dot{\bigcup }_{g\in G}\text{Isom}_{R}(E_{g^{-1}},E_{g})$ if and only if 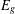$E_{g}$ is a connected commutative algebra or $E_{g}=E_{g}^{G_{r(g)}}\oplus E_{g}^{G_{r(g)}}$, where 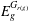$E_{g}^{G_{r(g)}}$ is connected, for all 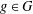$g\in G$.

Keywords

groupoidgroupoid Galois extensionpartial isomorphism

MSC classification

Primary: 13B05: Galois theory
Secondary: 18B40: Groupoids, semigroupoids, semigroups, groups (viewed as categories)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 59 - 68
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Bagio, D. and Paques, A., ‘Partial groupoid actions: globalization, Morita theory and Galois theory’, Comm. Algebra 40(10) (2012), 3658–3678.CrossRefGoogle Scholar
Brown, R., ‘Groupoids and Van Kampen’s theorem’, Proc. Lond. Math. Soc. (3) 17 (1967), 385–401.Google Scholar
Brown, R., ‘Fibrations of groupoids’, J. Algebra 15 (1970), 103–132.CrossRefGoogle Scholar
Brown, R., Topology and Groupoids (Booksurge, Charleston, SC, 2006).Google Scholar
Chase, S., Harrison, D. K. and Rosenberg, A., ‘Galois theory and Galois cohomology of commutative rings’, Mem. Amer. Math. Soc. 52 (1968), 1–19.Google Scholar
Heller, A., ‘On the homotopy theory of topogenic groups and groupoids’, Illinois J. Math. 24(4) (1980), 576–605.CrossRefGoogle Scholar
Lawson, M. V., Inverse Semigroups. The Theory of Partial Symmetries (World Scientific, London, 1998).CrossRefGoogle Scholar
Moerdijk, I. and Mrčun, J., Introduction to Foliations and Lie Groupoids (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Szeto, G. and Xue, L., ‘The Galois algebra with Galois group which is the automorphism group’, J. Algebra 293 (2005), 312–318.CrossRefGoogle Scholar