Hostname: page-component-6bf8c574d5-86b6f Total loading time: 0 Render date: 2025-03-07T10:52:13.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain locally nilpotent varieties of groups

Published online by Cambridge University Press:  17 April 2009

Alireza Abdollahi
Alireza Abdollahi
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan 81746-73441, Iran Institute for Studies in Theoretical Physics and Mathematics, Tehran, Iran, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let c ≥ 0, d ≥ 2 be integers and 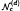be the variety of groups in which every d-generator subgroup is nilpotent of class at most c. N.D. Gupta asked for what values of c and d is it true that 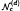is locally nilpotent? We prove that if c ≤ 2d + 2d−1 − 3 then the variety 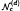is locally nilpotent and we reduce the question of Gupta about the periodic groups in 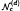to the prime power exponent groups in this variety.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 67 , Issue 1 , February 2003 , pp. 115 - 119
Copyright
Copyright © Australian Mathematical Society 2003

References

REFERENCES

[1]Endimioni, G., ‘Groups in which every d-generator subgroup is nilpotent of bounded class’, Quart. J. Math. Oxford (2) 46 (1995), 433–435.Google Scholar
[2]Gupta, N.D., ‘Certain locally metanilpotent varieties of groups’, Arch. Math. 20 (1969), 481–484.Google Scholar
[3]Heineken, H., ‘Engelsche Elemente der Länge drei’, Illinois J. Math. 5 (1961), 681–707.Google Scholar
[4]Lubotzky, A. and Mann, A., ‘Powerful p-groups. I. Finite groups’, J. Algebra 105 (1987), 484–505.CrossRefGoogle Scholar
[5]Newell, M.L., ‘On right-Engel elements of length three’, Proc. Roy. Irish Acad. Sect. A 96 (1996), 17–24.Google Scholar
[6]Plotkin, B.I., ‘On the nil-radical of a group’, Dokl. Akad. Nauk SSSR 98 (1954), 341–343.Google Scholar
[7]Robinson, D.J.S., A first course in the group theory, Graduate Texts in Mathematics 80, (Second edition) (Springer-Verlag, New York, 1996).Google Scholar
[8]Shalev, A., ‘Characterization of p-adic analytic groups in terms of wreath products’, J. Algebra 145 (1992), 204–208.Google Scholar
[9]Traustason, G., ‘On 4-Engel groups’, J. Algebra 178 (1995), 414–429.Google Scholar
[10]Vaughan-Lee, M., ‘Engel-4 groups of exponent 5’, Proc. London Math. Soc. (3) 74 (1997), 306–334.Google Scholar