Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T10:58:48.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain integrals for classes of p-valent meromorphic functions

Published online by Cambridge University Press:  17 April 2009

Vinod Kumar  and
S.L. Shukla
Vinod Kumar
Affiliation:
Department of Mathematics, Janta College, Bakewar 206124, Etawah (U.P.), India.
S.L. Shukla
Affiliation:
Department of Mathematics, Janta College, Bakewar 206124, Etawah (U.P.), India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we introduce two classes, namely Γp(m, M) and Σp(m, M), of functions

regular and p-valent in D − {0} where D = {z : |z| < 1}. We show that, for suitable choices of real constants α, β and γ, the integral operators of the form

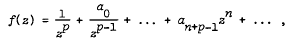
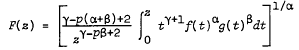
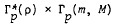map into 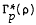, where 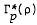is the class of p-valent meromorphically starlike functions of order ρ, 0 ≤ ρ < 1. For the classes Γp(m, M) and Σp(m, M), we obtain class preserving integral operators of the form

with suitable restrictions on real constants α and γ.

Our results generalize almost all known results obtained so far in this direction.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 25 , Issue 1 , February 1982 , pp. 85 - 97
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Bajpai, S.K., “A note on a class of meromorphic univalent functions”, Rev. Roumaine Math. Pures Appl. 22 (1977), 295–297.Google Scholar
[2]Dwivedi, S.P., “Certain classes of univalent functions and generalizations of functions with bounded boundary rotation” (PhD thesis, Indian Institute of Technology, Kanpur, India, 1975).Google Scholar
[3]Dwivedi, S.P., Bhargava, G.P. and Shukla, S.L., “On some classes of meromorphic univalent functions”, Rev. Roumaine Math. Pures Appl. 25 (1980), 209–215.Google Scholar
[4]Jack, I.S., “Functions starlike and convex of order α”, J. London Math. Soc. (2) 3 (1971), 469–474.CrossRefGoogle Scholar
[5]Jakubowski, Zbigniew Jerzy, “On the coefficients of starlike functions of some classes”, Ann. Polon. Math. 26 (1972), 305–313.Google Scholar
[6]Nehari, Zeev, Conformal mappings (McGraw Hill, New York, Toronto, London, 1952).Google Scholar
[7]Silverman, Herb, “Subclasses of starlike functions”, Rev. Roumaine Math. Pures Appl. 23 (1978), 1093–1099.Google Scholar