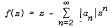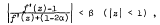Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mogra, M.L.
1984.
Analytic mappings with negative coefficients in the unit disc.
Bulletin of the Australian Mathematical Society,
Vol. 29,
Issue. 1,
p.
83.
Silverman, H
1984.
Order of starlikeness for multipliers of univalent functions.
Journal of Mathematical Analysis and Applications,
Vol. 103,
Issue. 1,
p.
48.
Silverman, Herb
1991.
A Survey with Open Problems on Univalent Functions Whose Coefficients are Negative.
Rocky Mountain Journal of Mathematics,
Vol. 21,
Issue. 3,
Srivastava, H.M.
and
Aouf, M.K.
1992.
A certain fractional derivative operator and its applications to a new class of analytic and multivalent functions with negative coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 171,
Issue. 1,
p.
1.
Assiri, E. Q.
and
Mogra, M. L.
1997.
A unified approach for univalent functions with negative coefficients using the Hadamard product.
Ukrainian Mathematical Journal,
Vol. 49,
Issue. 9,
p.
1305.
Orhan, Halit
and
Kiziltunç, Hükmi
2004.
A generalization on subfamily of p-valent functions with negative coefficients.
Applied Mathematics and Computation,
Vol. 155,
Issue. 2,
p.
521.
Aouf, M.K.
Silverman, H.
and
Srivastava, H.M.
2008.
Some families of linear operators associated with certain subclasses of multivalent functions.
Computers & Mathematics with Applications,
Vol. 55,
Issue. 3,
p.
535.
Frasin, B.A.
2008.
Generalization of partial sums of certain analytic and univalent functions.
Applied Mathematics Letters,
Vol. 21,
Issue. 7,
p.
735.
Srivastava, H. M.
Eker, Sevtap Sümer
and
Şeker, Bilal
2009.
A certain convolution approach for subclasses of analytic functions with negative coefficients.
Integral Transforms and Special Functions,
Vol. 20,
Issue. 9,
p.
687.
Ebadian, Ali
Aghalary, Rasoul
and
Najafzadeh, Shahram
2010.
Univalent Holomorphic Functions with Negative and Fixed Finitely Many Coefficients in terms of Generalized Fractional Derivative.
Kyungpook mathematical journal,
Vol. 50,
Issue. 4,
p.
499.
Deniz, Erhan
and
Orhan, Halit
2011.
Certain Subclasses of Multivalent Functions Defined by New Multiplier Transformations.
Arabian Journal for Science and Engineering,
Vol. 36,
Issue. 6,
p.
1091.
Yang, Jingyu
and
Li, Shuhai
2012.
Properties of Certain Subclass of Multivalent Functions with Negative Coefficients.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2012,
Issue. ,
p.
1.
Sharma, Poonam
and
Jain, Vanita
2013.
A Generalized Class of k-Starlike Functions Involving a Calculus Operator.
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences,
Vol. 83,
Issue. 3,
p.
247.
N. Magesh
and
V. Prameela
2013.
Certain subclasses of uniformly convex functions and corresponding class of starlike functions.
Malaya Journal of Matematik,
Vol. 1,
Issue. 1,
p.
18.
El-Ashwah, Rabha Mohamed
Aouf, Mohamed Kamal
Hassan, Ahmed
and
Hassan, Alaa
2014.
Certain Class of Analytic Functions Defined by Ruscheweyh Derivative with Varying Arguments.
Kyungpook mathematical journal,
Vol. 54,
Issue. 3,
p.
453.
Ahmad, M. Z.
Ibrahim, Rabha W.
and
Al-Janaby, Hiba F.
2016.
On some interesting properties for a new subclass of multivalent functions.
Asian-European Journal of Mathematics,
Vol. 09,
Issue. 01,
p.
1650027.
Frasin, B. A.
and
Gharaibeh, Mohammed M.
2020.
Subclass of analytic functions associated with Poisson distribution series.
Afrika Matematika,
Vol. 31,
Issue. 7-8,
p.
1167.
Malik, Faroze Ahmad
Dar, Nusrat Ahmed
and
Sharma, Chitaranjan
2021.
Certain Properties of a Generalized Class of Analytic Functions Involving Some Convolution Operator.
Earthline Journal of Mathematical Sciences,
p.
49.
Seoudy, T. M.
and
Shammaky, A. E.
2021.
Some properties for certain subclasses of multivalent functions associated with the $$q-$$difference linear operator.
Afrika Matematika,
Vol. 32,
Issue. 5-6,
p.
773.
Shammaky, Amnah E.
Frasin, Basem Aref
Seoudy, Tamer M.
and
Gao, Ji
2022.
Subclass of Analytic Functions Related with Pascal Distribution Series.
Journal of Mathematics,
Vol. 2022,
Issue. 1,