Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T16:35:34.322Z Has data issue: false hasContentIssue false
  • English
  • Français

CENTRALISERS IN THE INFINITE SYMMETRIC INVERSE SEMIGROUP

Part of: Semigroups

Published online by Cambridge University Press:  28 September 2012

JANUSZ KONIECZNY
JANUSZ KONIECZNY*
Affiliation:
Department of Mathematics, University of Mary Washington, Fredericksburg, VA 22401, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

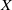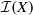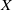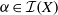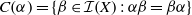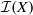For an arbitrary set $X$ (finite or infinite), denote by $\mathcal {I}(X)$ the symmetric inverse semigroup of partial injective transformations on $X$. For $ \alpha \in \mathcal {I}(X)$, let $C(\alpha )=\{ \beta \in \mathcal {I}(X): \alpha \beta = \beta \alpha \}$ be the centraliser of $ \alpha $ in $\mathcal {I}(X)$. For an arbitrary 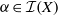$ \alpha \in \mathcal {I}(X)$, we characterise the transformations 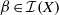$ \beta \in \mathcal {I}(X)$ that belong to 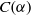$C( \alpha )$, describe the regular elements of 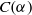$C(\alpha )$, and establish when 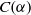$C( \alpha )$ is an inverse semigroup and when it is a completely regular semigroup. In the case where 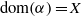$\operatorname {dom}( \alpha )=X$, we determine the structure of 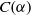$C(\alpha )$in terms of Green’s relations.

Keywords

symmetric inverse semigroupcentralisersregular elementsGreen’s relations

MSC classification

Secondary: 20M20: Semigroups of transformations, etc. 20M18: Inverse semigroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 462 - 479
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Araújo, J., Kinyon, M. & Konieczny, J., ‘Minimal paths in the commuting graphs of semigroups’, European J. Combin. 32 (2011), 178–197.CrossRefGoogle Scholar
[2]Araújo, J. & Konieczny, J., ‘Automorphism groups of centralizers of idempotents’, J. Algebra 269 (2003), 227–239.CrossRefGoogle Scholar
[3]Araújo, J. & Konieczny, J., ‘Semigroups of transformations preserving an equivalence relation and a cross-section’, Comm. Algebra 32 (2004), 1917–1935.CrossRefGoogle Scholar
[4]Araújo, J. & Konieczny, J., ‘General theorems on automorphisms of semigroups and their applications’, J. Aust. Math. Soc. 87 (2009), 1–17.CrossRefGoogle Scholar
[5]Araújo, J. & Konieczny, J., ‘Centralizers in the full transformation semigroup’, Semigroup Forum, to appear.Google Scholar
[6]Ayik, G., Ayik, H. & Howie, J. M., ‘On factorisations and generators in transformation semigroups’, Semigroup Forum 70 (2005), 225–237.CrossRefGoogle Scholar
[7]Bates, C., Bundy, D., Perkins, S. & Rowley, P., ‘Commuting involution graphs for symmetric groups’, J. Algebra 266 (2003), 133–153.CrossRefGoogle Scholar
[8]Higgins, P. M., ‘Digraphs and the semigroup of all functions on a finite set’, Glasgow Math. J. 30 (1988), 41–57.CrossRefGoogle Scholar
[9]Howie, J. M., Fundamentals of Semigroup Theory (Oxford University Press, New York, 1995).CrossRefGoogle Scholar
[10]Iranmanesh, A. & Jafarzadeh, A., ‘On the commuting graph associated with the symmetric and alternating groups’, J. Algebra Appl. 7 (2008), 129–146.CrossRefGoogle Scholar
[11]Jakubíková, D., ‘Systems of unary algebras with common endomorphisms. I, II’, Czechoslovak Math. J. 29(104) (1979), 406–420, 421–429.Google Scholar
[12]Kolmykov, V. A., ‘On the commutativity relation in a symmetric semigroup’, Siberian Math. J. 45 (2004), 931–934.CrossRefGoogle Scholar
[13]Kolmykov, V. A., ‘Endomorphisms of functional graphs’, Discrete Math. Appl. 16 (2006), 423–427.CrossRefGoogle Scholar
[14]Kolmykov, V. A., ‘On commuting mappings’, Mat. Zametki 86 (2009), 389–393 (in Russian).Google Scholar
[15]Konieczny, J., ‘Green’s relations and regularity in centralizers of permutations’, Glasgow Math. J. 41 (1999), 45–57.CrossRefGoogle Scholar
[16]Konieczny, J., ‘Semigroups of transformations commuting with idempotents’, Algebra Colloq. 9 (2002), 121–134.Google Scholar
[17]Konieczny, J., ‘Semigroups of transformations commuting with injective nilpotents’, Comm. Algebra 32 (2004), 1951–1969.CrossRefGoogle Scholar
[18]Konieczny, J., ‘Centralizers in the semigroup of injective transformations on an infinite set’, Bull. Austral. Math. Soc. 82 (2010), 305–321.CrossRefGoogle Scholar
[19]Konieczny, J., ‘Infinite injective transformations whose centralizers have simple structure’, Cent. Eur. J. Math. 9 (2011), 23–35.CrossRefGoogle Scholar
[20]Konieczny, J. & Lipscomb, S., ‘Centralizers in the semigroup of partial transformations’, Math. Japon. 48 (1998), 367–376.Google Scholar
[21]Levi, I., ‘Normal semigroups of one-to-one transformations’, Proc. Edinburgh Math. Soc. 34 (1991), 65–76.CrossRefGoogle Scholar
[22]Lipscomb, S., Symmetric Inverse Semigroups, Mathematical Surveys and Monographs, 46 (American Mathematical Society, Providence, RI, 1996).CrossRefGoogle Scholar
[23]Liskovec, V. A. & Feĭnberg, V. Z., ‘On the permutability of mappings’, Dokl. Akad. Nauk BSSR 7 (1963), 366–369 (in Russian).Google Scholar
[24]Novotný, M., ‘Sur un problème de la théorie des applications’, Publ. Fac. Sci. Univ. Massaryk 1953 (1953), 53–64 (Czech).Google Scholar
[25]Novotný, M., ‘Über Abbildungen von Mengen’, Pacific J. Math. 13 (1963), 1359–1369(in German).CrossRefGoogle Scholar
[26]Petrich, M., Inverse Semigroups (John Wiley & Sons, New York, 1984).Google Scholar
[27]Petrich, M. & Reilly, N. R., Completely Regular Semigroups (John Wiley & Sons, New York, 1999).Google Scholar
[28]Scott, W. R., Group Theory (Prentice Hall, Englewood Cliffs, NJ, 1964).Google Scholar
[29]Skornjakov, L. A., ‘Unary algebras with regular endomorphism monoids’, Acta Sci. Math. (Szeged) 40 (1978), 375–381.Google Scholar
[30]Szechtman, F., ‘On the automorphism group of the centralizer of an idempotent in the full transformation monoid’, Semigroup Forum 70 (2005), 238–242.CrossRefGoogle Scholar
[31]Weaver, M. W., ‘On the commutativity of a correspondence and a permutation’, Pacific J. Math. 10 (1960), 705–711.CrossRefGoogle Scholar